P=NP and Bitcoin
The present value of working on conjectures…
Anil Nerode of Cornell University has served over sixty years—he’s believed to be the longest such faculty member in university history. He helped found Cornell’s computer science department, advised more than 55 doctoral students—a Department of Mathematics record—and made important contributions to logic, mathematics, computer science, and more. He and Juris Hartmanis jointly oversaw Ken’s Mathematical Sciences Institute postdoc at Cornell in 1986–89.
I found it interesting that Anil has worked on teaching methods:
“I was educated at Chicago under the business of doing the cleanest, shortest expositions of absolutely everything,”
He has developed his own method: He now teaches in historical order. Translating ancient theories into modern notation allows him to show his students the origins of mathematics. This is a cool method.

|
| Cornell Chronicle source—our felicitations |
Anil has done extensive work in complex control systems, which is certainly a challenging area for an approach based on clarity and simplicity. He is often credited for co-creating, together with Wolf Kohn, an approach called hybrid systems theory. His partnership with Kohn has even extended to integrating quantum and macroscopic control mechanisms for magnetic batteries on many scales.
Conjectures Which Way?
Anil once said:
Being attached to a speculation is not a good guide to research planning. One should always try both directions of every problem. Prejudice has caused famous mathematicians to fail to solve famous problems whose solution was opposite to their expectations, even though they had developed all the methods required.
I blogged about this point in posts titled “We All Guessed Wrong” and “Even Great Mathematicians Guess Wrong”—and about other cases of surprises and about guessing the right side of conjectures.
But events this week have put a transverse thought into my head. The two sides of a conjecture may not be equal in their ramifications. This leads to a further weird thought:
Maybe the greatest overall value is in working hard on the side that you don’t want to be true—and hoping not to solve it.
The fact of Bitcoin hitting a new all-time high this week leads me to muse further about this.
Trillions
If you think you have a proof that P=NP then it is worth a lot of money. Well for sure, at least, you will get a prize like the Turing Award. But because it would break bitcoin and other digital monies you would possibly get into the thicket of billions of dollars. Maybe more like trillions.

|
| source |
Exactly what it would be worth to you, I don’t know. That’s a hypothetical. But there is a non-hypothetical that, from the understanding Ken and I have of how hedge transactions are valued, implies that one side of “P=NP” has clear and present monetary value:
What is the present value of not knowing that P=NP, and of exerting work that furthers the general sureness of this status?
A 2022 article titled “P = NP: The Dangling Blackhole Under Crypto” puts the stakes in stark terms:
P=NP is [about] whether a problem (in the case of Cryptocurrencies, a transaction) can be solved procedurally and systemically just as quickly as it can be verified with a hash. The security of the blockchain, such as [for] Bitcoin, is wholly dependent on the assumption that P does not equal NP. However, if P = NP is proven, the Bitcoin can be breached just as quickly as it can be authenticated.
A breach would have the kind of concrete effect we have in mind when we say, “from dollars to donuts…“—although the donuts involved could technically come from work like this:

|
| source |
Open Problems
Is it sensible to assign a present value to work on one side of the P=NP question? More than work that tries to establish the other side?


This is a well-known NP-complete problem:
We reduce this problem to MWX2SAT in polynomial time and so, MWX2SAT is in NP-complete as well. This is the definition:
INSTANCE: An -variable
-variable  formula with monotone clauses (meaning the variables are never negated) using logic operators
formula with monotone clauses (meaning the variables are never negated) using logic operators 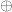 (instead of using the operator
(instead of using the operator  ) and a positive integer
) and a positive integer  .
.
QUESTION: Is there exists a satisfying truth assignment in which at most of the variables are true?
of the variables are true?
We prove this problem can be solved in polynomial time. See the proof here:
https://hal.science/hal-04420462
Moreover, we create our software programming implementation in Python:
https://github.com/frankvegadelgado/alma
Quote by Saint Augustine: The truth is like a lion. You don’t have to defend it. Let it loose. It will defend itself.
And how does it relate to cryptography?
Trying to convince the Google AI (Gemini) that P = NP
This is really hard to do 🙂
https://g.co/gemini/share/3a0f2d7cb012
My Question:
Does the phrase “either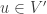 or
or 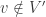 ” actually means (
” actually means (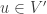 or
or 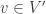 ) or (
) or ( or
or 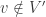 )?
)?
Google AI (Gemini) Answer:
Yes, the phrase “either u ∈ V’ or v ∉ V'” does mean the same as:
(u ∈ V’ or v ∈ V’) or (u ∉ V’ or v ∉ V’)
Here’s the breakdown:
The original statement offers two possibilities:
However, the intent is to convey that only one of these conditions needs to be true, not both.
Therefore, rewriting it as two separate “or” statements clarifies this meaning:
So, both the original statement and the rewritten form using two “or” statements express the same logical concept: at least one of u or v must satisfy the condition related to V’, but not necessarily both.
https://g.co/gemini/share/5ca2bd4abb59
Albert Einstein Quote: “I want to know what God thinks. The rest are details.”
I rewrite another version after my interaction with the Google AI (Gemini):
https://www.preprints.org/manuscript/201908.0037/v10
In the previous version v10, we create two ways to prove that MWX2SAT is in P. In this version v11, we just remove the one that is flawed and keep the single one that is correct.
https://www.preprints.org/manuscript/201908.0037/v11
Dear Fellow,
I would be very grateful if you as an expert in the field would consider reviewing this publication:
Publication title: “Note for the P versus NP Problem”
https://www.scienceopen.com/document/read?id=94777eae-28c7-402d-8e6b-8e882de7a3f6
To review, go to that page and click on the “Review” button or consult the details about the reviewing process at ScienceOpen:
https://about.scienceopen.com/peer-review-guidelines
ScienceOpen enables every researcher to openly review any paper which has been submitted or published elsewhere.
Thank you very much also for your cooperation. I look forward to your review!
With kind regards,
Frank Vega
We improved the Lemma 1 (that is the polynomial time reduction from K-CLOSURE to MWX2SAT (Lemma 1)) and added a Discussion section with some important highlights in this last new version:
https://www.preprints.org/manuscript/201908.0037/v12
Dear Fellow,
I would be very grateful if you as an expert in the field would consider reviewing this publication:
Publication title: “Note for the P versus NP Problem” (Second Version)
https://www.scienceopen.com/document/read?vid=5e6e97ed-697f-4685-a43b-6c48e598af02
To review, go to that page and click on the “Review” button or consult the details about the reviewing process at ScienceOpen:
https://about.scienceopen.com/peer-review-guidelines
ScienceOpen enables every researcher to openly review any paper which has been submitted or published elsewhere.
Thank you very much also for your cooperation. I look forward to your review!
With kind regards,
Frank Vega
This the last version of the proof that P = NP:
https://www.techrxiv.org/users/258307/articles/716221-note-for-the-p-versus-np-problem
This version is as perfect as possible!
The problem with using Bitcoin in this value estimation is that none of the “value” of Bitcoin would actually be captured if the hashing algorithm were compromised. The price of Bitcoin would just become zero as everyone fanatically tries to shed their coins. The first person to notice their coins being stolen or the mining difficulty skyrocketing would sound the alarm and it’d be over before the attacker could cash out to fiat.
Yes, but we mean the present value of increasing the level of assurance that this scenario will not happen.
Yesterday a reliable proof of The Millennium Prize Problem (P vs NP) has been published!
We define the Monotone Weighted Xor 2-satisfiability problem (MWX2SAT). We show this problem is NP-complete and P at the same time. In this way, we prove the complexity classes P and NP are equals using a feasible and efficient algorithm.
https://ipipublishing.org/index.php/ipil/article/view/92
I copied this highlight text from a source on internet: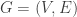 , create a DAG
, create a DAG  where there is one node for each vertex of
where there is one node for each vertex of  and one node for each edge of
and one node for each edge of  . If
. If  is the node correspond to edge
is the node correspond to edge  then make
then make  be preceded by
be preceded by  in
in  (i.e. the new nodes created from the vertices). Therefore, k-CLIQUE becomes equivalent to deciding whether or not there is a closure with
(i.e. the new nodes created from the vertices). Therefore, k-CLIQUE becomes equivalent to deciding whether or not there is a closure with  nodes. Frank’s problem (MWX2SAT) can be easily reduced to k-MWX2SAT over the same kind of instances but with satisfying truth assignments of exactly
nodes. Frank’s problem (MWX2SAT) can be easily reduced to k-MWX2SAT over the same kind of instances but with satisfying truth assignments of exactly  true variables. The rest of Frank’s proof could remain the same!
true variables. The rest of Frank’s proof could remain the same!
————————————————
I think Frank’s proof could work! Here’s the reduction from k-CLIQUE to k-CLOSURE. Given graph
—————————————————
https://ipipublishing.org/index.php/ipil/article/view/92
I think I found another version of the reduction from CLIQUE to K-CLOSURE by myself (without citing any external source). Given a graph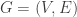 , we remove the disconnected vertices in
, we remove the disconnected vertices in  and every pair of vertices
and every pair of vertices  and
and  such that they only are endpoints of a single edge
such that they only are endpoints of a single edge  . Note that, finding a clique of size
. Note that, finding a clique of size  is trivial. Next, we create a line graph
is trivial. Next, we create a line graph  of
of  . Each edge in
. Each edge in  is a pair of edges from
is a pair of edges from  that have a shared vertex. This vertex is included in the edge representation of
that have a shared vertex. This vertex is included in the edge representation of  , for example, as
, for example, as  in
in  where
where  is the shared vertex between the two edges
is the shared vertex between the two edges 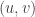 and
and 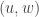 in
in  . We are always able to find this line graph
. We are always able to find this line graph  in polynomial time due to our initial redundant vertices removal process in
in polynomial time due to our initial redundant vertices removal process in  . Now, finding a clique of size
. Now, finding a clique of size  in
in  is equivalent to finding a closure of size
is equivalent to finding a closure of size  in
in  .
.
https://ipipublishing.org/index.php/ipil/article/view/92
I have received some negative comments about my P=NP proof from detractors. Basically, they said that Garey and Johnson’s book should be wrong about the statement and definition of K-CLOSURE as an NP-complete problem. Since Garey and Johnson’s book mentioned that CLIQUE can be reduced to K-CLOSURE in polynomial time, I tried to find that reduction myself. I think my previous comments were wrong on that topic. I need time to improve it since my P=NP proof took me too long to achieve despite its simplicity. I also considered the possibility that the error was on my part, which could only mean that I had misunderstood the use of the words which I took to be equivalent to Boolean XOR operation in the book. There are contexts where it is used as OR in English, but we looked through the entire book and authors Garey and Johnson always used that statement in the book as the Boolean XOR operation. If that’s not the case, then my P=NP proof should be correct for sure!
which I took to be equivalent to Boolean XOR operation in the book. There are contexts where it is used as OR in English, but we looked through the entire book and authors Garey and Johnson always used that statement in the book as the Boolean XOR operation. If that’s not the case, then my P=NP proof should be correct for sure!
https://ipipublishing.org/index.php/ipil/article/view/92
There are some people who speculate that the definition used by Garey and Johnson is ambiguous to justify that my article should not be correct. Here is the definition of K-CLOSURE, but each vertex must have equal weight to match the K-CLOSURE definition of NP-Completeness by Garey and Johnson in their book “Computers and Intractability: A Guide to the Theory of NP-Completeness” (1979):
https://cstheory.stackexchange.com/questions/40447/min-weight-k-closure-on-dag
I think K-CLOSURE is NP-hard due to a reduction from K-Bipartite Expansion based on a comment on the Stack Exchange link I shared above. Given a bipartite -vertex graph
-vertex graph  and positive integers
and positive integers  and
and  , the problem K-Bipartite Expansion consists in deciding whether there is a
, the problem K-Bipartite Expansion consists in deciding whether there is a  -subset of
-subset of  with exactly
with exactly  neighbors in
neighbors in  . To reduce it to the K-CLOSURE problem, we create a
. To reduce it to the K-CLOSURE problem, we create a 
 with two levels by duplicating each vertex in
with two levels by duplicating each vertex in  exactly
exactly 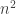 times and directing all edges of
times and directing all edges of  to the new set
to the new set  . Given this scenario, we ask for the existence of a closure with exactly
. Given this scenario, we ask for the existence of a closure with exactly  vertices. This follows from the fact that a solution with
vertices. This follows from the fact that a solution with  vertices in
vertices in  implies that there must exist
implies that there must exist  predecessor vertices in
predecessor vertices in  by the definition of a closure set. Note that, it is impossible that it could exist
by the definition of a closure set. Note that, it is impossible that it could exist  vertices for
vertices for 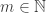 in the closure which belong to the bipartite set
in the closure which belong to the bipartite set  since the cardinality of
since the cardinality of  must be less than
must be less than  . Here is the NP hardness proof for Bipartite Expansion where we can infer the decision variant of K-Bipartite Expansion:
. Here is the NP hardness proof for Bipartite Expansion where we can infer the decision variant of K-Bipartite Expansion:
https://www.semanticscholar.org/paper/Hardness-of-Bipartite-Expansion-Khot-Saket/6c292af8b5eb9b3dc3b8ad216833063941b5c9be?p2df
My comments above did not match Garey and Johnson’s definition of NP-Completeness K-CLOSURE. Indeed, they emphasized that for all edges in a digraph
in a digraph  either
either 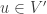 or
or 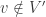 for a closure set
for a closure set 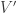 of at most
of at most  vertices which also means that either (
vertices which also means that either (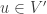 and
and 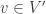 ) or (
) or ( and
and 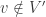 ). Let me try one more time to finish this challenge suggested by people who want to refute my P=NP article because they do not believe in the Queyranne’s reduction used by Garey and Johnson in their book! The CLIQUE problem (a variant of optimization) consists of finding the maximum clique in a given undirected graph
). Let me try one more time to finish this challenge suggested by people who want to refute my P=NP article because they do not believe in the Queyranne’s reduction used by Garey and Johnson in their book! The CLIQUE problem (a variant of optimization) consists of finding the maximum clique in a given undirected graph 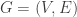 . First, we initialize an integer variable
. First, we initialize an integer variable 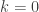 . Next, we create a digraph
. Next, we create a digraph  as follows: for each pair of vertices
as follows: for each pair of vertices  we always create two new vertices
we always create two new vertices  and
and  and added two new edges
and added two new edges  whenever
whenever  . Every time we create these two new vertices and edges whenever there is a missing edge in
. Every time we create these two new vertices and edges whenever there is a missing edge in  , we increment our variable
, we increment our variable  . By incrementing
. By incrementing  by 2, we guarantee that vertices
by 2, we guarantee that vertices  and
and  do not coincide in the maximum clique. Finally, we reduce CLIQUE (in its optimization variant) to find a maximum closure set into
do not coincide in the maximum clique. Finally, we reduce CLIQUE (in its optimization variant) to find a maximum closure set into  of at most
of at most  vertices. If you believe if my reduction or Queyranne’s reduction is correct, then you just only need to check the remaining steps of my P = NP proof in this published article:
vertices. If you believe if my reduction or Queyranne’s reduction is correct, then you just only need to check the remaining steps of my P = NP proof in this published article:
https://ipipublishing.org/index.php/ipil/article/view/92
The author of the reference [Queyranne, 1976] that Garey and Johnson used in their book “Computers and Intractability: A Guide to the Theory of NP-Completeness” (1979) for the definition of NP-completeness of K-CLOSURE is still alive. I will suggest to the naysayers to question him the polynomial reduction from CLIQUE to K-CLOSURE instead of making the mistake of trying to do what he already did or assuming that they committed a mistake in the definition of K-CLOSURE. Here is the link to his website
https://www.researchgate.net/profile/Maurice-Queyranne
We define for
for 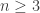 (using the Dedekind
(using the Dedekind 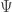 function). We prove the inequality
function). We prove the inequality  holds for
holds for  big enough, where
big enough, where  is the primorial of order
is the primorial of order  . This implies the Riemann hypothesis is true.
. This implies the Riemann hypothesis is true.
https://www.preprints.org/manuscript/202002.0379/v10
We define the Monotone Weighted Xor 2-satisfiability problem (MWX2SAT). We show this problem is NP-complete and P at the same time. In this way, we prove the complexity classes P and NP are equals using a feasible and efficient algorithm.
https://www.preprints.org/manuscript/201908.0037/v14
A Note on Riemann Hypothesis (authors: Gemini [Google AI] and me)
In trenches we toil, unseen, unheard,
Building bridges, mending every word.
Weaving tapestries of care and trust,
For the weary, the lost, the filled with dust.
We plant the seeds, the ones that grow,
For a world where kindness starts to flow.
We’ll keep on striving, though voices fall flat,
For the good of the many, where truly it matters at that.
Though fame may elude, and praise be thin,
We’ll find our solace in the battles we win.
————————————————-
https://www.preprints.org/manuscript/202002.0379/v11
Last version of my proof of Riemann Hypothesis sent for peer-review:
https://www.preprints.org/manuscript/202002.0379/v12
One of the biggest unsolved mysteries in computer science is the P versus NP problem. This work proposes that a specific NP-complete problem, MWX2SAT, can be solved efficiently. In this way, we prove that P is equal to NP. This solution might have also a huge impact in mathematics.
https://ipipublishing.org/index.php/ipil/article/view/92
Wiles’ proof of Fermat’s Last Theorem, while successful, relied on modern tools far beyond Fermat’s claimed approach in terms of complexity. The present work potentially offers a solution which is closer in spirit to Fermat’s original idea.
https://www.preprints.org/manuscript/202109.0480/v6
People continue arguing and sending messages to me about the NP-Completeness K-CLOSURE defined by Garey and Johnson. Garey and Johnson emphasized that for all edges of a digraph
of a digraph  in K-CLOSURE either
in K-CLOSURE either 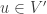 or
or 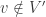 which also means that either (
which also means that either (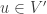 and
and 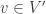 ) or (
) or ( and
and 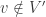 ). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Frequently, their convinced discourse assures that the empty set is a trivial counterexample of its correctness. They don’t realize that the Queyranne’s reduction necessarily implies that a closure
). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Frequently, their convinced discourse assures that the empty set is a trivial counterexample of its correctness. They don’t realize that the Queyranne’s reduction necessarily implies that a closure 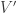 of size at most
of size at most  can be transformed into a clique of size at least
can be transformed into a clique of size at least  (or
(or  , etc) in a reduction from CLIQUE (input: an undirected graph
, etc) in a reduction from CLIQUE (input: an undirected graph 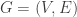 ) to K-CLOSURE (output: a digraph
) to K-CLOSURE (output: a digraph  ). Hence, an empty closure can imply the maximum clique in a complete graph.
). Hence, an empty closure can imply the maximum clique in a complete graph.
If you believe the Queyranne’s reduction is correct, then you just only need to check the remaining steps of my P = NP proof in the following published article:
https://ipipublishing.org/index.php/ipil/article/view/92
Garey and Johnson emphasized that for all edges of a digraph
of a digraph  in K-CLOSURE either
in K-CLOSURE either 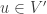 or
or 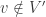 which also means that either (
which also means that either (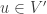 and
and 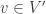 ) or (
) or ( and
and 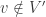 ). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Some people were kind and normal regarding this topic, but some other people are daunted and really naysayers about it (that’s why I don’t waste too much time on this) but at some point, I believe I need to put an end into this story. A variant of CLIQUE problem consists in finding a clique of size “exactly”
). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Some people were kind and normal regarding this topic, but some other people are daunted and really naysayers about it (that’s why I don’t waste too much time on this) but at some point, I believe I need to put an end into this story. A variant of CLIQUE problem consists in finding a clique of size “exactly”  in a given undirected graph
in a given undirected graph  . Then, we create a digraph
. Then, we create a digraph  as follows: for every pair of vertices
as follows: for every pair of vertices  (we also consider the case of
(we also consider the case of  ), we create two new vertices
), we create two new vertices  (we also guarantee that
(we also guarantee that  ) and add two new edges
) and add two new edges  whenever
whenever  or
or 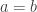 . Finally, we reduce the finding of a clique in
. Finally, we reduce the finding of a clique in  of size “exactly”
of size “exactly”  into the finding of a closure set
into the finding of a closure set 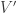 in
in  of size “exactly”
of size “exactly”  (we conveniently take
(we conveniently take  as 0). Solving the classic variant of CLIQUE problem consists in finding a solution to a clique of size “exactly” a natural number between
as 0). Solving the classic variant of CLIQUE problem consists in finding a solution to a clique of size “exactly” a natural number between  and
and  where
where  is the cardinality function.
is the cardinality function.
If you believe the Queyranne’s reduction or mine is correct, then you just only need to check the remaining steps of my P = NP proof in the published article:
https://ipipublishing.org/index.php/ipil/article/view/92
My last reduction is not correct but it should be quite close to the correct one!
Indeed, my last reduction might be correct if we allow the closure set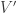 in
in  to take a size “exactly between”
to take a size “exactly between”  and
and  .
.
I mean “exactly between” and $3 \cdot k + 2 \cdot {k \choose 2} + \mid E \mid – {k \choose 2}$.
and $3 \cdot k + 2 \cdot {k \choose 2} + \mid E \mid – {k \choose 2}$.
Garey and Johnson emphasized that for all edges of a digraph
of a digraph  in K-CLOSURE either
in K-CLOSURE either 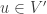 or
or 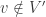 which also means that either (
which also means that either (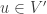 and
and 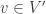 ) or (
) or ( and
and 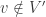 ). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Let me put an end at this story! The CLIQUE problem consists in finding a clique of size at least
). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Let me put an end at this story! The CLIQUE problem consists in finding a clique of size at least  in a given undirected graph
in a given undirected graph 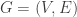 . Then, we create a digraph
. Then, we create a digraph  as follows: for every pair of vertices
as follows: for every pair of vertices  (we assume that
(we assume that 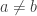 ), we create two new vertices
), we create two new vertices  (we also guarantee that
(we also guarantee that  ) and add two new edges
) and add two new edges  whenever
whenever  . Finally, we reduce the finding of a clique in
. Finally, we reduce the finding of a clique in  of size at least
of size at least  into the finding of a closure set
into the finding of a closure set 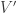 in
in  of size at least
of size at least  (we conveniently ignore the case when
(we conveniently ignore the case when 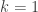 ). We can use the Garey and Johnson book’s definition of its problem K-CLOSURE using the complement graph of
). We can use the Garey and Johnson book’s definition of its problem K-CLOSURE using the complement graph of  and finding a closure set
and finding a closure set  of size at most
of size at most  , where
, where  means the size of the set of vertices
means the size of the set of vertices  in both graph.
in both graph.
If you believe the Queyranne’s reduction or mine is correct, then you just only need to check the remaining steps of my P = NP proof in the published article:
https://ipipublishing.org/index.php/ipil/article/view/92
I mean we can use the Garey and Johnson book’s definition of its problem K-CLOSURE using the complement graph of , following the same steps to create the digraph
, following the same steps to create the digraph  and finding a closure set
and finding a closure set  in
in 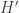 of size at most
of size at most  , where
, where  means the size of the set of vertices
means the size of the set of vertices  in
in  .
.
[Final] Garey and Johnson emphasized that for all edges of a digraph
of a digraph  in K-CLOSURE either
in K-CLOSURE either 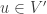 or
or 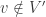 which also means that either (
which also means that either (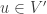 and
and 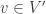 ) or (
) or ( and
and 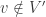 ). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Let me put an end at this story! The CLIQUE problem consists in finding a clique of size at least
). Most people think Garey and Johnson were wrong and the cite [Queyranne, 1976] was a miscommunication. Let me put an end at this story! The CLIQUE problem consists in finding a clique of size at least  in a given undirected graph
in a given undirected graph 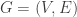 . Then, we create a digraph
. Then, we create a digraph  as follows: for every pair of vertices
as follows: for every pair of vertices  (we assume that
(we assume that 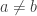 ), we create two new vertices
), we create two new vertices  (we also guarantee that
(we also guarantee that  ) and add two new edges
) and add two new edges  whenever
whenever  . Finally, we reduce the finding of a clique in
. Finally, we reduce the finding of a clique in  of size at least
of size at least  into the finding of a closure set
into the finding of a closure set 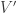 in
in  of size at least
of size at least  (we conveniently ignore the case when
(we conveniently ignore the case when 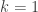 ). We can use the Garey and Johnson book’s definition of its problem K-CLOSURE using the complement graph of
). We can use the Garey and Johnson book’s definition of its problem K-CLOSURE using the complement graph of  , following the same steps to create the digraph
, following the same steps to create the digraph  and finding a closure set
and finding a closure set  in
in 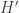 of size at most
of size at most  , where
, where  is the number of vertices in
is the number of vertices in  .
.
If you believe the Queyranne’s reduction or mine is correct, then you just only need to check the remaining steps of my P = NP proof in the published article:
https://ipipublishing.org/index.php/ipil/article/view/92
The problem, which involves determining if a clique of size at least
problem, which involves determining if a clique of size at least  exists in a given undirected graph
exists in a given undirected graph 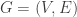 , can be reduced to the problem of finding a closure set
, can be reduced to the problem of finding a closure set 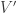 in a constructed directed graph
in a constructed directed graph  of size at most
of size at most  , where
, where  is the number of vertices and
is the number of vertices and  is the number of edges of
is the number of edges of  . The directed graph
. The directed graph  is created by introducing
is created by introducing  new vertices
new vertices  and
and  for each pair of vertices
for each pair of vertices  and adding
and adding  new edges
new edges  and
and  whenever
whenever  or
or 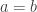 . Note that, an empty closure can imply the maximum clique in a complete graph
. Note that, an empty closure can imply the maximum clique in a complete graph  . Given that
. Given that  is an
is an  -complete problem, it follows that
-complete problem, it follows that  is also
is also  -complete.
-complete.
If you believe the Queyranne’s reduction or mine is correct, then you just only need to check the remaining steps of my P = NP proof in the published article:
https://ipipublishing.org/index.php/ipil/article/view/92
Garey and Johnson defined K-CLOSURE such that for any edge (u, v) in the directed graph, either node u is in the set V’ or node v is not in V’. This implies that either both nodes are in V’ or both are not in V’. Our previous work in IPI Letters presented a polynomial-time algorithm for K-CLOSURE. While no errors have been identified in this work, many believe that Garey and Johnson’s original definition was incorrect, and their citation of Queyranne was a misunderstanding. Many argue that the empty set serves as a simple counterexample to Garey and Johnson’s definition of K-CLOSURE. This paper proposes that K-CLOSURE is actually an NP-complete problem, which would imply that P equals NP.
https://www.researchgate.net/publication/384017297_Solving_NP-complete_Problems_Efficiently
While no errors have been identified in my polynomial-time algorithm for K-CLOSURE, many believe that Garey and Johnson’s original definition was incorrect. This published article proposes that K-CLOSURE is actually in NP-complete.
https://ipipublishing.org/index.php/ipil/article/view/122
Definitely solved MWX2SAT using maximum matching (a polynomial time solution for a proven NP-complete by a reduction from K-CLOSURE).
https://github.com/frankvegadelgado/alma
This algorithm takes time O(number_of_nodes ** 3) [1].
[1] “Efficient Algorithms for Finding Maximum Matching in Graphs”, Zvi Galil, ACM Computing Surveys, 1986.
We create a new version where the Monotone Weighted Xor 2-satisfiability problem (MWX2SAT) consists in deciding whether any of its instances contains a satisfying truth assignment in which k of the variables are true. These instances are defined as a n-variable 2CNF formula with monotone clauses (meaning the variables are never negated) using XOR logic operators (instead of using the operator OR) and a positive integer k. We show that the Monotone Weighted Xor 2-satisfiability problem (MWX2SAT) is NP-complete and P at the same time. Certainly, we make a polynomial time reduction from every directed graph and positive integer k in the K-CLOSURE problem to an instance of MWX2SAT. In this way, we show that MWX2SAT is also an NP-complete problem. Moreover, we create and implement a polynomial time algorithm which decides the instances of MWX2SAT. Consequently, we prove that P = NP.
k of the variables are true. These instances are defined as a n-variable 2CNF formula with monotone clauses (meaning the variables are never negated) using XOR logic operators (instead of using the operator OR) and a positive integer k. We show that the Monotone Weighted Xor 2-satisfiability problem (MWX2SAT) is NP-complete and P at the same time. Certainly, we make a polynomial time reduction from every directed graph and positive integer k in the K-CLOSURE problem to an instance of MWX2SAT. In this way, we show that MWX2SAT is also an NP-complete problem. Moreover, we create and implement a polynomial time algorithm which decides the instances of MWX2SAT. Consequently, we prove that P = NP.
https://ipipublishing.org/index.php/ipil/article/view/92
In this new version of my article proving that P = NP, the difference with the previous version is that I used “at least” instead of “at most”. Everything is fine now (even the deployment to GitHub with Python). I think the key to being able to solve it was first in implementing my solution on my computer (detecting the error) and second in the confidence/faith in success: Everything conspires in favor when you firmly believe that you can do it (when you take it for granted), in the illusion of the result (feeding hope: visualizing the achievement) and in the awareness that the universe is friendly (it helps you in your purpose) seen from any point of view (religious or not).
https://ipipublishing.org/index.php/ipil/article/view/92
INSTANCE: A directed graph and a positive integer
and a positive integer  .
.
QUESTION: Is there set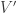 of at least
of at least  vertices such that for all
vertices such that for all  either
either 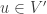 or
or 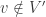 ?
?
REMARKS: The problem is
problem is  -complete. This follows from the fact that it is equivalent to the
-complete. This follows from the fact that it is equivalent to the  -complete
-complete  problem, where the target closure size is simply complemented by reversing the direction of all edges in the graph.
problem, where the target closure size is simply complemented by reversing the direction of all edges in the graph.
A -vertex set
-vertex set 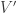 is a “closure” if, for every edge
is a “closure” if, for every edge 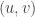 in the graph, either both vertices
in the graph, either both vertices  and
and  are in
are in 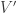 or are not in
or are not in 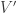 . In other words, a closure is a subset of vertices where, if one vertex is included, all vertices that have edges pointing directly to it must also be included. The closure property holds for graphs of any size, and it is “hereditary”, meaning that if a graph has the closure property, then any subgraph of that graph also has the closure property~\cite{GJ79}. This property is a fundamental characteristic of closures. Furthermore, we can efficiently determine if a given subgraph has the closure property using a polynomial-time algorithm. This means that checking for the closure property is computationally feasible, even for large graphs. The
. In other words, a closure is a subset of vertices where, if one vertex is included, all vertices that have edges pointing directly to it must also be included. The closure property holds for graphs of any size, and it is “hereditary”, meaning that if a graph has the closure property, then any subgraph of that graph also has the closure property~\cite{GJ79}. This property is a fundamental characteristic of closures. Furthermore, we can efficiently determine if a given subgraph has the closure property using a polynomial-time algorithm. This means that checking for the closure property is computationally feasible, even for large graphs. The  problem involves finding the smallest possible subset of vertices in a directed graph that, when removed, leaves a graph with the closure property. This problem is equivalent to the
problem involves finding the smallest possible subset of vertices in a directed graph that, when removed, leaves a graph with the closure property. This problem is equivalent to the  , which is known to be
, which is known to be  -complete [1]. Therefore, the
-complete [1]. Therefore, the  problem is also
problem is also  -complete, meaning that it is impossible to find an efficient algorithm for solving it unless
-complete, meaning that it is impossible to find an efficient algorithm for solving it unless  .
.
[1] Mihalis Yannakakis. 1978. Node-and edge-deletion NP-complete problems. In Proceedings of the tenth annual ACM symposium on Theory of computing (STOC ’78). Association for Computing Machinery, New York, NY, USA, 253–264.
See polynomial time solution to in the following paper:
in the following paper:
https://ipipublishing.org/index.php/ipil/article/view/92
I recently shared a published version of an article in the journal IPI Letters about one of the millennium problems. I wanted to share with you the fact that the new and old version published in IPI Letters was wrong (or rather incomplete). I was able to fix and extend it and manage to reach a state of that result that keeps me optimistic and happy. Here I share it with you:
https://www.preprints.org/manuscript/202409.2053/v3
In 2022, I published my article on the Riemann hypothesis in The Ramanujan Journal (a high-impact journal) and recently I completed it, achieving the demonstration of the complete hypothesis. Even though the difference is basically 2 more pages, I wish it had occurred to me at the time, but it was only now that I managed to notice the improvement:
https://www.preprints.org/manuscript/202409.1972/v1
It also happened to me when I was debating with another colleague about Fermat’s Last Theorem, a solution to this theorem came to me that seems beauty, brilliant and very, very simple. Although it may seem incredible, I have faith in this demonstration of Fermat’s Last Theorem (perhaps I have a little less confident on this one, but I still have a hope according to my intuition):
https://www.preprints.org/manuscript/202109.0480/v9
A polynomial time algorithm for an NP-complete problem described at [https://www.preprints.org/manuscript/202409.2053/v3]:
https://cs.stackexchange.com/questions/169897/a-2-coloring-of-a-bipartite-graph-such-that-one-of-the-partitions-contains-exact
If an NP-complete problem could be solved efficiently, it would imply that all problems in NP could be solved efficiently, proving P equals NP. This research proposes that EXACT CLOSURE, a notoriously difficult NP-complete problem, can be solved efficiently, thereby potentially establishing the equivalence of P and NP. This work is an expansion and refinement of the article “Note for the P versus NP problem”, published in IPI Letters.
https://www.preprints.org/manuscript/202409.2053/v5
This research proposes that a notoriously difficult NP-complete problem can be solved efficiently, thereby potentially establishing the equivalence of P and NP. This work is an expansion and refinement of the article “Note for the P versus NP problem”, published in IPI Letters.
https://www.preprints.org/manuscript/202409.2053/v8
● Efficiently solves SAT in polynomial time.
● Breaks the long-standing complexity barrier.
● Revolutionizes fields like AI, cryptography, and optimization.
https://www.linkedin.com/pulse/sat-polynomial-time-proof-p-np-frank-vega-ltfie
Solve SAT in polynomial time via maximum independent set in line graphs.
https://www.preprints.org/manuscript/202409.2053/v17
A better approximate solution to the Minimum Vertex Cover Problem distributed via pip: https://pypi.org/project/capablanca/
We present a polynomial-time algorithm achieving an approximation ratio below √2 for Minimum Vertex Cover Problem, providing strong evidence that P = NP and disproving the Unique Games Conjecture. The polynomial time solution was implemented in Python and it is available at
https://pypi.org/project/capablanca/
Breakthrough Algorithm Solves the Unsolvable: A Giant Leap Towards P = NP!
Discover the 4/3-Approximation for MVC That’s Redefining the Boundaries of Computer Science!
Why This Matters?
– Challenges P = NP: Our algorithm provides strong evidence that P could equal NP, solving computationally hard problems with near-optimal efficiency.
– Defies the Unique Games Conjecture: This breakthrough suggests that many optimization problems may have better solutions than previously thought, revolutionizing theoretical computer science.
– Real-World Impact: From AI to logistics, this discovery paves the way for faster, smarter solutions to some of the most challenging problems in tech and beyond.
https://pypi.org/project/capablanca/
Discover a new 7/5-Approximation for MVC That’s Redefining the Boundaries of Computer Science!
Why This Matters?
1. Challenges P = NP,
2. Defies the Unique Games Conjecture,
3. Real-World Impact.
Distributed via PyPI:
https://pypi.org/project/varela/
Disproving the Unique Games Conjecture! This work provides a strong evidence that the Unique Games Conjecture does not hold. This is very positive approach since if the conjecture would be true, then this would imply the hardness of approximating solutions to many other important problems in various fields of mathematics, including graph theory, optimization, and even aspects of geometry. BTW, I removed the flawed extension of this result for proving P=NP.
https://pypi.org/project/varela/
The Dominating Set Problem is a fundamental problem in graph theory and combinatorial optimization, with applications in network design, social network analysis, and resource allocation. The algorithm employs an efficient algorithm to compute an approximate Dominating Set for an undirected graph using the NetworkX library. A Dominating Set is a subset of vertices such that every vertex in the graph is either in the subset or adjacent to at least one vertex in the subset. Since finding the exact minimum Dominating Set is NP-hard, the algorithm employs a 8-approximation approach based on a minimum maximal matching. The algorithm first validates the input graph to ensure it is undirected and non-empty. Isolated nodes are removed as they cannot contribute to a connected Dominating Set. The core of the algorithm uses NetworkX’s “min_maximal_matching” function. The resulting matching is converted into a Dominating Set by including all nodes in the matched edges. Next, we iteratively remove redundant vertices from the initial candidate dominating set. This approach guarantees polynomial runtime while maintaining reasonable approximation quality. This work contributes to the growing body of research on approximation algorithms for NP-hard problems, providing strong evidence that P = NP.
https://pypi.org/project/baldor/
Leading AI systems have reportedly confirmed the validity of my P=NP proof and provided a detailed analysis of its theoretical foundations:
https://www.linkedin.com/posts/frank-vega-delgado_vertex-cover-problem-new-insights-critique-activity-7305610255227404289-y9Kq?utm_source=share&utm_medium=member_desktop&rcm=ACoAAA3ojloBlOVpZezqUMtGhzfTLS7gJSDjw14
This algorithm resolves the NP-Hard Minimum Dominating Set Problem in quadratic time, suggesting P = NP and delivering practical benefits across diverse fields, including artificial intelligence, medicine, and impact in the industries.
https://dev.to/frank_vega_987689489099bf/polynomial-time-algorithm-for-mds-p-np-1ln6
I proposed an approximate solution to the NP-Hard Minimum Dominating Set Problem (MDS), which has shown promising experimental results. The experimental findings demonstrate a 2-approximation ratio for this problem, providing compelling evidence that P=NP.
https://dev.to/frank_vega_987689489099bf/a-2-approximation-algorithm-for-dominating-sets-1aga
This result decisively refutes the conjecture, enhancing our insight into prime distribution and the behavior of the zeta function’s zeros through analytic number theory.
https://www.preprints.org/manuscript/202504.0246/v1