A Lemma on Factoring
And a dilemma on making further use of it
Gary Miller is a Professor of Computer Science at Carnegie Mellon University. He is best known for the Miller-Rabin primality test, which was cited in awarding him the 2003 ACM Paris Kanellakis Award along with Michael Rabin, Robert Solovay, and Volker Strassen. He has, however, been active in many other areas. His publications page has the best database functionality of any I know, and needs it.
Today Ken and I wish to talk about a result that evolved from Gary’s classic 1975 primality-testing paper into Section 2 of an equally classic 1986 joint work with Eric Bach and Jeffrey Shallit on factoring. That paper also ascribes it to Douglas L. Long. We wonder if it can be evolved further.
I still recall the night I heard about Gary’s great result. This was before e-mail and of course the Internet. Social media meant phone calls or even letters. David Dobkin had heard about the result, and we were both at a party on a Saturday night when he grabbed me, and took me aside—the party was loud–and told me about Gary’s theorem on primality testing. I was immediately excited, a breakthrough? Certainly if one believes the Extended Riemann Hypothesis as used in the paper to get an time algorithm, where
is the number of digits in the number being tested, and the tilde ignores factors of
. The unconditional primality test of Manindra Agrawal, Neeraj Kayal, and Nitin Saxena, which was
since improved to
, was definitely hailed as one, including the 2006 Gödel prize.
Last year, Gary was hailed here for a “theoretical breakthrough…with enormous practical potential” on the solving of linear systems of equations from symmetric diagonally dominant matrices. The paper is joint with Ioannis Koutis and Richard Peng, and appeared at FOCS 2010. The CMU press release notes that Gaussian elimination “was first published by Chinese mathematicians 2,000 years ago”—a case of “everything being named after Gauss.”
The Result
We will state the result only for the case where
are two distinct odd primes. This shows off the method, avoids messy notation, and is the most important case anyway. In crypto-systems that use factoring as a hardness assumption this is usually the case that they care about.
The related significance of the result is expressed by the title of the referenced paper by Long: “Random equivalence of factorization and computation of orders.” This is the equivalence used implicitly in Peter Shor’s famous paper on factoring by quantum computers. We have not been able to trace Long’s paper beyond the “to appear” citations. In any event, Shor cites the 1976 journal version of Miller’s paper for this equivalence.
Lemma 1 Suppose we are given integers
and
such that
where
and
are odd primes, and
is a multiple of
. Then we can factor
in randomized polynomial time.
The proof below is a slight simplification of the one in Section 2 of the 1986 paper, but still strikes us as not the proof from The Book. We thought you might like looking at it.
Factoring Via GCD
There really is one theme that is used over and over in most methods of factoring: try to construct an integer so that
divides
and
does not. Then the value of
will equal
, and
is factored. Of course the roles of
and
can be exchanged—the key is that only one prime divides
and the other does not. Note that the ancient algorithm of Euclid computes
in time that is a small power of the number of digits in
and
, thus in polynomial time.
Let’s look at how this strategy factors provided we know a multiple
of
.
Define to be true when only one of
and
divides
. Also define
to be true when both
and
are odd numbers. The rationale for these definitions is the following two lemmas:
Lemma 2 There is a randomized algorithm
that factors
with probability at least one-half, provided
is true.
Proof. Assume that is true, and
divides
. Pick a random
in
, and compute
. We claim that at least half the time this is a factor of
. Picking
by the Chinese Remainder Theorem (CRT) is equivalent to picking
modulo each prime separately. Now
, since
and
divides
. So we need to show that
is true only at most half the time. Since does not divide
there is some
so that
. This uses that
is a cyclic group of order
. But then the set of
so that
is a proper subgroup, and thus has at most half the elements modulo
. This proves the lemma.
Lemma 3 There is a randomized algorithm
that factors
with probability at least one-half, provided
is true.
Proof. Assume that is true. Pick a random
in
, and compute
. We claim that at least half the time this is a factor of
. Since
is true there is an
so that
and
is odd, and there is an
so that
and
is also odd. Now picking
randomly means that at least half the time
will be a quadratic residue modulo one of the primes and a non-residue modulo the other. So assume that
is a quadratic residue modulo
and a non-residue modulo
. Then,
by the famous Euler criterion. The last step is to note that by definition of and
this is the same as:
Putting This Together
Recall that we start with an —any
—such that
divides
. Note that we don’t yet know what
is, we just know that it is among the divisors of the
we have.
Our goal is to find —possibly another
—so that
or
is true. Define
, and let
be such that
is an odd integer. We run
and
for all
. If any yields a factor we are done. Otherwise, we try the process again. The final point is that this process works at least one-half the time.
Let’s prove that. Initially divides
by assumption. If
does not divide
then
is true and we are done. Note that since
is odd, neither divides it. Hence there must exist a least
such that
and
both divide
but do not both divide
. If exactly one divides
then
holds and again we are done.
So suppose neither divides . Then we have integers
and
such that
Necessarily and
are both odd, else one of
or
would divide
. Thus
is true. This each run of the above process has at least a one-half chance to factor.
Open Problems
Is there a way, given knowledge of , to improve the probability of hitting an
such that one of
or
divides
? Of course this is equivalent to improving the heuristic odds on factoring.
[fixed AKS names, clarified last eqn in Lemma 3, fixed CMU link]



The names should be Neeraj Kayal and Nitin Saxena.
Whoops! Tushar Saxena is someone I knew (of) while he was at Albany. Thanks. Meanwhile, I was occupied with Mac Firefox momentarily displaying the raw LaTeX code rather than rendering it, but it is now OK again.
To me and
and  may be ambiguous but most intuitively parses like
may be ambiguous but most intuitively parses like 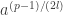 and
and 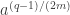 . I assume you mean what would be clearer as
. I assume you mean what would be clearer as 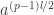 and
and 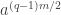 .
.
Ørjan Johansen,
Good point. We should have fixed that. Of course it only divide by 2. Thanks.
Fixed—thanks. Actually, here’s a weird “excuse” while tired: I was trying to work out whether only one evaluation of B^*(r_{k-1},M) might be needed in the algorithm as originally written, so mentally I was seeing powers of 2 in those denominators…
Very nice post.
But I can’t resist: Joel David Hamkins has, in my biased opinion, a slightly better publication page.
By “better” I only mean the database functionality, of course.
“But I can’t resist: Joel David Hamkins has, in my biased opinion, a slightly better publication page.”
Not bad. But nobody beats Neal Young:
http://www.cs.ucr.edu/~neal/publications
“Last year, Gary was hailed here”
The link at the word “here” seems to be broken.
Fixed—the “http://” was missing. Thanks. Alternate, perhaps more permanent, link in the CMU archives here.
When I was an undergrad in the 70s Miller was working on graph embedding, and had some nice papers on efficient ways to embed planar graphs. At the time, I got the impression he was moving in the direction of graph isomorphism, but apparently he changed course interestingly.
I don’t know why the period r got by quantum computing can be divided by p-1. Could you say more about it? I can only infer that r divides (p-1)(q-1).