Riemann Hypothesis—Why So Hard?
“If I were to awaken after having slept a thousand years, my first question would be: has the Riemann Hypothesis been proven?” — David Hilbert

|
| Steklov Institute memorial page |
Sergei Voronin was an expert in number theory, who studied the Riemann zeta function, but who sadly died young over twenty years ago. We discussed his amazing 1975 result about the Riemann zeta function here. Others call the result the amazing theorem. I (Dick) am getting old—I almost forgot that we did a post on his theorem again over four years ago.
Today I thought we would recall his theorem, sketch why the theorem is true, and then discuss some extensions.
Starting with Alan Turing we have been interested in universal objects. Turing famously proved that there are universal machines: these can simulate any other machine on any input. Martin Davis has an entire book on this subject.

|
Universal objects are basic to complexity theory. Besides Turing’s notion, a universal property is key to the definition of NP-complete. A set in NP is NP-complete provided all other sets in NP can be reduced to
in polynomial time. Michael Nielsen once began a discussion of universality in this amusing fashion:
Imagine you’re shopping for a new car, and the salesperson says, “Did you know, this car doesn’t just drive on the road.” “Oh?” you reply. “Yeah, you can also use it to do other things. For instance, it folds up to make a pretty good bicycle. And it folds out to make a first-rate airplane. Oh, and when submerged it works as a submarine. And it’s a spaceship too!”
Voronin’s Insight
In 1975 Voronin had the brilliant insight that the Riemann zeta function has an interesting universality property. Roughly speaking, it says that a wide class of analytic functions can be approximated by shifts
with real
. Recall
for , and it has an analytic extension for all other values but
.
The intense interest in the function started in 1859 with Bernhard Riemann’s breakthrough article. This was the first statement of what we call the Riemann Hypothesis (RH).
In over a century of research on RH before Voronin’s theorem, many identities, many results, many theorems were proved about the zeta function. But none saw that the function was universal before Voronin. Given the zeta function’s importance in understanding the structure of prime numbers this seems to be surprising.
Before we define the universal property I thought it might be useful to state a related property that the function has:
Theorem 1 Suppose that
is a polynomial so that for all
,
Then
is identically zero.
Since is a single variable, this says that
and its derivatives
and
do not satisfy any polynomial relationship. This means intuitively that
must be hypertranscendental. Let’s now make this formal.
Voronin’s Theorem
Here is his theorem:
Theorem 2 Let
. Let
be an analytic function that never is zero for
. Then for any
there is a real
so that
See the paper “Zeroes of the Riemann zeta-function and its universality,” by Ramunas Garunkstis, Antanas Laurincikas, and Renata Macaitiene, for a detailed modern discussion of his theorem.

|
Note that the theorem is not constructive. However, the values of that work have a positive density—there are lots of them. Also note the restriction that
is never zero is critical. Otherwise one would be able to show that the Riemann Hypothesis is false. In 2003, Garunkstis et al. did prove a constructive version, in a paper titled, “Effective Uniform Approximation By The Riemann Zeta-Function.”
Voronin’s Proof
The key insight is to combine two properties of the zeta function: The usual definition with the Euler product. Recall the Riemann zeta-function has an Euler product expression
where runs over prime numbers. This is valid only in the region
, but it makes sense in a approximate sense in the critical strip:
Then take logarithms and since are linearly independent over
, we can apply the Kronecker approximation theorem to obtain that any target function
can be approximated by the above finite truncation. This is the basic structure of the proof.
Open Problems
Voronin’s insight was immediately interesting to number theorists. Many found new methods for proving universality and for extending it to other functions. Some methods work for all zeta-functions defined by Euler products. See this survey by Kohji Matsumoto and a recent paper
by Hafedh Herichi and Michel Lapidus, the latter titled “Quantized Number Theory, Fractal Strings and the Riemann Hypothesis: From Spectral Operators to Phase Transitions and Universality.”
Perhaps the most interesting question is:
Can universality be used to finally unravel the RH?
See Paul Gauthier’s 2014 IAS talk, “Universality and the Riemann Hypothesis,” for some ideas.
[fixed missing line at end]


I’m really proud of have been working with you in a paper about the Riemann Hypothesis. Unfortunately, we have stopped the communication, but I hope some day we can finally continue on this. From our interchange, I learned a lot, principally in how to organize better the ideas (I need to learn more on that). You prefer to be only mentioned in the acknowledgements, that’s why I have to remove all your contributions and only pick some tiny things from our collaboration (for just to be honest with you). I wish that you could know that my invitation to work together on this is still open: this work can be improved much more until make it a perfect and verified proof (this has not been validated yet). This is all I have moved on these few past weeks:
https://doi.org/10.5281/zenodo.3648511
What do you think?
Nice introductory article for the general reader in the theory of universality of the Riemann zeta function. One comment I have is that on the last paragraph on “Open Problems” the last phrase is not typed properly, I guess you meant to say: “ See Khoji’s Matsumoto’s survey and also the work done by Hafedh Herichi and Michel Lapidus on quantizing the universality theorem of Voronin”. I suggest to fix this phrase, since in his survey, K. Matsumoto does not discuss the research work of Herichi and Lapidus on a quantum analog of the universality theorem of Voronin involving using truncated spectral operators. Overall a very nice art introductory article !
Thanks! I suspect a line of text was lost owing to a technical glitch.
There is universality. It is “topological quantization” where “critical line” is a boundary of certain manifold and pole at 1 is Arnold tongue. I think I’m 3 theorem away from RH. First — If a submanifold is constructable by local zeta function(“emergent acting potential” so to say) and has equalized action to outside and inside to zero, then meeting “super-secret” condition results in existence of self-adjoint unbounded operator that constructs this manifold out of nothingness, it emerges, so to say, and this operator is linear. Also, it cannot be wandering. Second — For any topological cycle on “topological quanta” there does exist algebraic cycle that has certain rotation number(zero maybe? I’m a bit struggling with this condition) if a set of topological quanta is closed for particular topological cycle. Using the fact that “critical line” is a boundary of a manifold we show that critical line is “fixable”(we can repair it) and bring zeroes to its place by moving zeroes in relation to each other, it is like if RH is false then we can come up with better function that does the same and has its all zeroes on the line, this criteria is super easy. Third — there does exist cycle on “topological quanta” of a form p + 2 = p (twin prime conjecture) and it occurs infinitely often. Assuming that it is false we show that in this case Arnold tongue would make pole at 1 finite value and therefore strip RZF of its analytic continuation. And then we state that pole at 1 implies that our set of “topological quanta” is a self-boundary of certain manifold that gets created by RZF in an act of “self-emergence” and that if any such cycle P+n1=n2 would fail it would imply that n1 or n2 is not in N. I call it “criteria of incremental stability”. You can imagine natural line to be a topology based vector(with of quanta 1 and repeat it infinitely often for all numbers on the vector) and prime numbers to be a directional quanta of this vector in all possible directions and for each P there does exist similar rerepresentaion on quanta of this quantized vector and it all unites in continuous “thing”. It is all going to be super-confusing, I know, but imagine zero-knowledge proofs of action in dynamical systems. You give me DS and claim that you have seen action in it. How do I verify without obtaining knowledge about your proof that it is right? I’m just checking that “our topological quanta” coincide that’s it. And PvsNP is harder then this because it requires measuring “density of cycles” in all possible ways, I think I’m going to give up on P!=NP because of this. By the end of this year I will, maybe, post my paper or go to prison for criticizing Putin. I just have no formal education and don’t think that anybody will be interested in a reading of my fabrication, still the process of making one is quite interesting!
Zeta universality does have the proof of P vs NP. However, writing it out in detail is NP hard!
If NP complete languages are subset of Indexed languages which are subset of Context sensitive languages which are subset of Turing complete languages which humans are capable of why is P vs NP important?
What if RH has a simple proof? Check this out:
Short Note on the Riemann Hypothesis
Robin criterion states that the Riemann Hypothesis is true if and only if the inequality $\sigma(n) 5040$, where $\sigma(n)$ is the sum-of-divisors function and $\gamma \approx 0.57721$ is the Euler-Mascheroni constant. This is known as the Robin inequality. We know that the Robin inequality is true for all $n > 5040$ which are not divisible by $2$. In addition, we prove the Robin inequality is true for all $n > 5040$ which are divisible by $2$. In this way, we show the Robin inequality is true for all $n > 5040$ and thus, the Riemann Hypothesis is true.
https://figshare.com/articles/preprint/Short_Note_on_the_Riemann_Hypothesis/16337109
A peer-reviewed RH proof was accepted by the conference:
http://icrdm.org/index.php/icrdm
which was actually an extension of my article “Robin’s criterion on
divisibility” published by The Ramanujan Journal (03 May 2022):
https://link.springer.com/article/10.1007/s11139-022-00574-4
In that article, Lipton made an important contribution and for that
reason he appears at the acknowledgements. Here, it is the possible conference presentation:
https://www.cambridge.org/engage/coe/article-details/62fdb7b8f3b96608f4b1ad18
Best wishes…
I have simplified much more the article and the presentation in my ResearchGate Project:
https://www.researchgate.net/project/The-Riemann-Hypothesis
This time the presentation and article are more short and concise.
Yesterday, I made my presentation:
Note on the Riemann Hypothesis
at the International Conference on Recent Developments in Mathematics (ICRDM 2022). This is the layout I used:
https://www.researchgate.net/publication/362887695_Note_on_the_Riemann_Hypothesis_International_Conference_on_Recent_Developments_in_Mathematics_ICRDM_2022
This is a groundbreaking result if correct. This would not have been possible without Lipton’s collaboration on the main reference I used.
Thank you…
I added a single detail at the end of my manuscript accepted by the conference ICRDM 2022. It is not a major or minor fix, it is just a simple detail to be able to publish it in the best possible way in the Springer journal.
https://www.researchgate.net/publication/363133519_Note_on_the_Riemann_Hypothesis
This version could appear at the end of this year in the flagship journal of Trends in Mathematics (Springer).
We define a new sequence smaller than the one used in the manuscript published by The Ramanujan Journal. In this way, the final conclusions are more precise.
https://www.researchgate.net/publication/363263423_Note_on_the_Riemann_Hypothesis
We hope this time it will be much better.
Final peer-reviewed version accepted by The Conference ICRDM, 2022:
https://www.researchgate.net/publication/363332962_Note_on_the_Riemann_Hypothesis
In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.14387.30244
In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
https://dx.doi.org/10.13140/RG.2.2.14387.30244
Thanks in advance.
We improved the last theorem.
https://dx.doi.org/10.13140/RG.2.2.27910.65600
Robin’s criterion states that the Riemann Hypothesis is true if and only if the inequality {\sigma(n) 5040}, where {\sigma(n)} is the sum-of-divisors function of {n} and {\gamma \approx 0.57721} is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of {n \mapsto \frac{\sigma(n)}{n}}. In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
https://dx.doi.org/10.13140/RG.2.2.27910.65600
Robin’s criterion states that the Riemann Hypothesis is true if and only if the inequality , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of
is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of  . In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
. In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
https://dx.doi.org/10.13140/RG.2.2.27910.65600
Thanks…
Robin’s criterion states that the Riemann Hypothesis is true if and only if the inequality holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of
is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of  . In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
. In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
https://dx.doi.org/10.13140/RG.2.2.27910.65600
Thanks in advance…
Robin’s criterion states that the Riemann Hypothesis is true if and only if the inequality holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of
is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of  . In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
. In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
https://dx.doi.org/10.13140/RG.2.2.20885.19689
Robin’s criterion states that the Riemann Hypothesis is true if and only if the inequality holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of
is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of  . In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
. In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
https://dx.doi.org/10.13140/RG.2.2.30958.08003
This is the version to be submitted to Springer.
Robin’s criterion states that the Riemann Hypothesis is true if and only if the inequality holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of
is the Euler-Mascheroni constant. We require the properties of superabundant numbers, that is to say left to right maxima of  . In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
. In this note, using Robin’s inequality on superabundant numbers, we prove that the Riemann Hypothesis is true. This proof is an extension of the article “Robin’s criterion on divisibility” published by The Ramanujan Journal on May 3rd, 2022.
https://dx.doi.org/10.13140/RG.2.2.30958.08003
The Holy Grail of Mathematics
A trustworthy proof for the Riemann hypothesis has been considered as the Holy Grail of Mathematics by several authors. The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Let
. Let 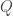 be the set of prime numbers
be the set of prime numbers  satisfying the inequality
satisfying the inequality  with the product extending over all prime numbers
with the product extending over all prime numbers  that are less than or equal to
that are less than or equal to  , where
, where  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant,  is the Chebyshev function and
is the Chebyshev function and  is the natural logarithm. If the Riemann hypothesis is false, then there are infinitely many prime numbers
is the natural logarithm. If the Riemann hypothesis is false, then there are infinitely many prime numbers  outside and inside of
outside and inside of 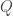 . In this note, we obtain a contradiction when we assume that there are infinitely many prime numbers
. In this note, we obtain a contradiction when we assume that there are infinitely many prime numbers  outside of
outside of 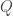 . By reductio ad absurdum, we prove that the Riemann hypothesis is true.
. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.22556.97929
Thanks in advance…
The Holy Grail of Mathematics (A Millennium Prize Problem)
A trustworthy proof for the Riemann hypothesis has been considered as the Holy Grail of Mathematics by several authors. The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Let
. Let 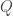 be the set of prime numbers
be the set of prime numbers  satisfying the inequality
satisfying the inequality  with the product extending over all prime numbers
with the product extending over all prime numbers  that are less than or equal to
that are less than or equal to  , where
, where  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant,  is the Chebyshev function and
is the Chebyshev function and  is the natural logarithm. If the Riemann hypothesis is false, then there are infinitely many prime numbers
is the natural logarithm. If the Riemann hypothesis is false, then there are infinitely many prime numbers  outside and inside of
outside and inside of 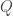 . In this note, we obtain a contradiction when we assume that there are infinitely many prime numbers
. In this note, we obtain a contradiction when we assume that there are infinitely many prime numbers  outside of
outside of 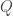 . By reductio ad absurdum, we prove that the Riemann hypothesis is true.
. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.15964.05763
Thanks in advance…
Trivial results extended on the paper:
https://dx.doi.org/10.13140/RG.2.2.15964.05763
Note that,
since for :
:
where .
.
However, we know that
for several values of z.
Certainly, when then,
then,
since for :
:
In this way, we know that
for several values of while
while  could be large enough.
could be large enough.
The End.
Robin’s criterion on superabundant numbers
A trustworthy proof for the Riemann hypothesis has been considered as the Holy Grail of Mathematics by several authors. The Riemann hypothesis is the assertion that all non-trivial zeros of the Riemann zeta function have real part . Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality
. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality  holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of
is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of  . If the Riemann hypothesis is false, then there are infinitely many superabundant numbers
. If the Riemann hypothesis is false, then there are infinitely many superabundant numbers  such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.15538.07368
Thank you for any possible feedback…
Robin’s criterion on superabundant numbers
A trustworthy proof for the Riemann hypothesis has been considered as the Holy Grail of Mathematics by several authors. The Riemann hypothesis is the assertion that all non-trivial zeros of the Riemann zeta function have real part . Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality
. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality  holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of
is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of  . If the Riemann hypothesis is false, then there are infinitely many superabundant numbers
. If the Riemann hypothesis is false, then there are infinitely many superabundant numbers  such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.18683.80165
Thanks in advance…
I’m interested in getting any possible feedback on:
Robin’s criterion on superabundant numbers.
A trustworthy proof for the Riemann hypothesis has been considered as the Holy Grail of Mathematics by several authors. The Riemann hypothesis is the assertion that all non-trivial zeros of the Riemann zeta function have real part . Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality
. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality  holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of
is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of  . If the Riemann hypothesis is false, then there are infinitely many superabundant numbers
. If the Riemann hypothesis is false, then there are infinitely many superabundant numbers  such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.36404.73603
Thanks in advance…
ResearchGate Project on the Riemann hypothesis (articles and preprints):
https://www.researchgate.net/project/The-Riemann-Hypothesis
“I think I’m making progress….”
Riemann hypothesis on odd perfect numbers
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . The Riemann hypothesis is considered by many to be the most important unsolved problem in pure mathematics. Let
. The Riemann hypothesis is considered by many to be the most important unsolved problem in pure mathematics. Let  denote the sum-of-divisors function
denote the sum-of-divisors function  . An integer
. An integer  is perfect if
is perfect if  . It is unknown whether any odd perfect numbers exist. Leonhard Euler stated: “Whether
. It is unknown whether any odd perfect numbers exist. Leonhard Euler stated: “Whether  there are any odd perfect numbers is a most difficult question”. We require the properties of superabundant numbers, that is to say left to right maxima of
there are any odd perfect numbers is a most difficult question”. We require the properties of superabundant numbers, that is to say left to right maxima of  . We also use Ramanujan’s old notes which were published in 1997 annotated by Jean-Louis Nicolas and Guy Robin. There are several statements equivalent to the famous Riemann hypothesis. In this note, conditional on Riemann hypothesis, we prove that there are not infinitely many odd perfect numbers.
. We also use Ramanujan’s old notes which were published in 1997 annotated by Jean-Louis Nicolas and Guy Robin. There are several statements equivalent to the famous Riemann hypothesis. In this note, conditional on Riemann hypothesis, we prove that there are not infinitely many odd perfect numbers.
https://dx.doi.org/10.13140/RG.2.2.28212.73605
Thanks…
Riemann hypothesis on odd perfect numbers
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . The Riemann hypothesis is considered by many to be the most important unsolved problem in pure mathematics. Let
. The Riemann hypothesis is considered by many to be the most important unsolved problem in pure mathematics. Let  denote the sum-of-divisors function
denote the sum-of-divisors function  . An integer
. An integer  is perfect if
is perfect if  . It is unknown whether any odd perfect numbers exist. Leonhard Euler stated: “Whether
. It is unknown whether any odd perfect numbers exist. Leonhard Euler stated: “Whether  there are any odd perfect numbers is a most difficult question”. We require the properties of superabundant numbers, that is to say left to right maxima of
there are any odd perfect numbers is a most difficult question”. We require the properties of superabundant numbers, that is to say left to right maxima of  . We also use Robin’s criterion and Ramanujan’s old notes which were published in 1997 annotated by Jean-Louis Nicolas and Guy Robin. There are several statements equivalent to the famous Riemann hypothesis. In this note, conditional on Riemann hypothesis, we prove that there is no odd perfect number.
. We also use Robin’s criterion and Ramanujan’s old notes which were published in 1997 annotated by Jean-Louis Nicolas and Guy Robin. There are several statements equivalent to the famous Riemann hypothesis. In this note, conditional on Riemann hypothesis, we prove that there is no odd perfect number.
https://dx.doi.org/10.13140/RG.2.2.27452.51848
Best wishes…
Robin’s criterion on superabundant numbers (A Millennium Prize Problem)
A trustworthy proof for the Riemann hypothesis has been considered as the Holy Grail of Mathematics by several authors. The Riemann hypothesis is the assertion that all non-trivial zeros of the Riemann zeta function have real part . Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality
. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality  holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of
is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of  . If the Riemann hypothesis is false, then there are infinitely many superabundant numbers
. If the Riemann hypothesis is false, then there are infinitely many superabundant numbers  such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
such that the Robin's inequality is unsatisfied. In this note, we show that the Robin's inequality always holds for large enough superabundant numbers. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.25470.05445
Thanks in advance…
Riemann hypothesis on odd perfect numbers
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . The Riemann hypothesis is considered by many to be the most important unsolved problem in pure mathematics. Let
. The Riemann hypothesis is considered by many to be the most important unsolved problem in pure mathematics. Let  denote the sum-of-divisors function
denote the sum-of-divisors function  . An integer
. An integer  is perfect if
is perfect if  . It is unknown whether any odd perfect numbers exist. Leonhard Euler stated: “Whether
. It is unknown whether any odd perfect numbers exist. Leonhard Euler stated: “Whether 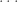 there are any odd perfect numbers is a most difficult question”. We require the properties of superabundant numbers, that is to say left to right maxima of
there are any odd perfect numbers is a most difficult question”. We require the properties of superabundant numbers, that is to say left to right maxima of  . We also use Robin’s criterion and Ramanujan’s old notes which were published in 1997 annotated by Jean-Louis Nicolas and Guy Robin. There are several statements equivalent to the famous Riemann hypothesis. In this note, conditional on Riemann hypothesis, we prove that there is no odd perfect number.
. We also use Robin’s criterion and Ramanujan’s old notes which were published in 1997 annotated by Jean-Louis Nicolas and Guy Robin. There are several statements equivalent to the famous Riemann hypothesis. In this note, conditional on Riemann hypothesis, we prove that there is no odd perfect number.
https://dx.doi.org/10.13140/RG.2.2.13490.07363
Thanks in advance…
Robin’s Inequality for Superabundant Numbers (A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . There are several statements equivalent to the famous Riemann hypothesis. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality
. There are several statements equivalent to the famous Riemann hypothesis. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality  holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of
is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of  . It is well-known that the smallest counterexample of the Robin's inequality greater than
. It is well-known that the smallest counterexample of the Robin's inequality greater than  must be a superabundant number. In this note, we prove that the Robin's inequality holds for all superabundant numbers greater than
must be a superabundant number. In this note, we prove that the Robin's inequality holds for all superabundant numbers greater than  . By reductio ad absurdum, we prove that the Riemann hypothesis is true.
. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.13817.75365
Thanks in advance…
Robin’s Inequality for Superabundant Numbers (A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . There are several statements equivalent to the famous Riemann hypothesis. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality
. There are several statements equivalent to the famous Riemann hypothesis. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality  holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of
is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of  . It is well-known that the smallest counterexample of the Robin's inequality greater than
. It is well-known that the smallest counterexample of the Robin's inequality greater than  must be a superabundant number. In this note, we prove that the Robin's inequality holds for all superabundant numbers greater than
must be a superabundant number. In this note, we prove that the Robin's inequality holds for all superabundant numbers greater than  . By reductio ad absurdum, we prove that the Riemann hypothesis is true.
. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.18746.06086
Now, I think I have RH in my hands.
What do you think?
Thanks in advance…
On Solé and Planat criterion for the Riemann hypothesis
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . This is one of the Clay Mathematics Institute’s Millennium Prize Problems. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that the Riemann hypothesis is true if and only if the inequality
. This is one of the Clay Mathematics Institute’s Millennium Prize Problems. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that the Riemann hypothesis is true if and only if the inequality  holds for all prime numbers
holds for all prime numbers  , where
, where  is the Chebyshev function,
is the Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 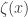 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. Let
is the natural logarithm. Let  denote the sum-of-divisors function of
denote the sum-of-divisors function of  . We also require the properties of superabundant numbers, that is to say left to right maxima of
. We also require the properties of superabundant numbers, that is to say left to right maxima of  . In this note, using Solé and Planat criterion on superabundant numbers, we prove that the Riemann hypothesis is true.
. In this note, using Solé and Planat criterion on superabundant numbers, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.10010.11200
Thanks in advance…
Riemann Hypothesis on Grönwall’s Function (A Millennium Prize Problem)
Grönwall’s function is defined for all natural numbers
is defined for all natural numbers 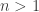 by
by  where
where  is the sum of the divisors of
is the sum of the divisors of  and
and  is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of
is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of  . We also use the colossally abundant and hyper abundant numbers. A number
. We also use the colossally abundant and hyper abundant numbers. A number  is said to be colossally abundant if, for some
is said to be colossally abundant if, for some 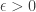 ,
,  for all
for all 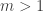 . Let us call hyper abundant an integer
. Let us call hyper abundant an integer  for which there exists
for which there exists  such that
such that  for all
for all 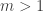 . The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part
. The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part  . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers  such that
such that  . In addition, we prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers
. In addition, we prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers  with any parameter
with any parameter  .
.
https://dx.doi.org/10.13140/RG.2.2.11805.79843
Thanks in advance…
Riemann Hypothesis on Grönwall’s Function (A Millennium Prize Problem)
Grönwall’s function is defined for all natural numbers
is defined for all natural numbers 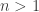 by
by  where
where  is the sum of the divisors of
is the sum of the divisors of  and
and  is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of
is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of  . We also use the colossally abundant and hyper abundant numbers. A number
. We also use the colossally abundant and hyper abundant numbers. A number  is said to be colossally abundant if, for some
is said to be colossally abundant if, for some 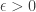 ,
,  for all
for all 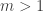 . Let us call hyper abundant an integer
. Let us call hyper abundant an integer  for which there exists
for which there exists  such that
such that  for all
for all 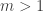 . The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part
. The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part  . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers  such that
such that  . In addition, we prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers
. In addition, we prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers  with any parameter
with any parameter  .
.
https://dx.doi.org/10.13140/RG.2.2.22658.56002
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function (A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the Chebyshev function,
is the Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 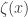 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://dx.doi.org/10.13140/RG.2.2.25992.70408
Thanks in advance…
Robin’s Inequality for Superabundant Numbers (A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . There are several statements equivalent to the famous Riemann hypothesis. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality
. There are several statements equivalent to the famous Riemann hypothesis. Robin’s criterion states that the Riemann hypothesis is true if and only if the inequality  holds for all natural numbers
holds for all natural numbers  , where
, where  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of
is the natural logarithm. We require the properties of superabundant numbers, that is to say left to right maxima of  . It is well-known that the smallest counterexample of the Robin's inequality greater than
. It is well-known that the smallest counterexample of the Robin's inequality greater than  must be a superabundant number. In this note, we prove that the Robin's inequality holds for all superabundant numbers greater than
must be a superabundant number. In this note, we prove that the Robin's inequality holds for all superabundant numbers greater than  . By reductio ad absurdum, we prove that the Riemann hypothesis is true.
. By reductio ad absurdum, we prove that the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.12439.85923
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the Chebyshev function,
is the Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 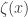 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://hal.archives-ouvertes.fr/hal-03827536/document
Now, the Riemann hypothesis is solved!!!
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 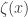 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://easychair.org/publications/preprint_open/XRMwc
Update on solution of the Riemann hypothesis!!!
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 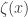 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://dx.doi.org/10.13140/RG.2.2.25992.70408
Last update on solution of the Riemann hypothesis!!!
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
New DOI on last update on solution of the Riemann hypothesis!!!
https://dx.doi.org/10.13140/RG.2.2.25992.70408/1
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 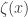 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://easychair.org/publications/preprint_open/hTGC
Official and not removable last update on solution of the Riemann hypothesis!!!
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 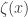 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://dx.doi.org/10.13140/RG.2.2.25992.70408/2
I made it more understandable now…
Riemann Hypothesis on Grönwall’s Function
(A Millennium Prize Problem)
Grönwall’s function is defined for all natural numbers
is defined for all natural numbers 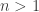 by
by  where
where  is the sum of the divisors of
is the sum of the divisors of  and
and  is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of
is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of  . We also use the colossally abundant and hyper abundant numbers. A number
. We also use the colossally abundant and hyper abundant numbers. A number  is said to be colossally abundant if, for some
is said to be colossally abundant if, for some 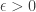 ,
,  for all
for all 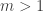 . Let us call hyper abundant an integer
. Let us call hyper abundant an integer  for which there exists
for which there exists  such that
such that  for all
for all 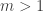 . The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part
. The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part  . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 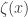 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://easychair.org/publications/preprint_open/rnSr
Official and not removable last update on solution of the Riemann hypothesis!!!
Thanks in advance…
Riemann Hypothesis on Grönwall’s Function (A Millennium Prize Problem)
Grönwall’s function is defined for all natural numbers
is defined for all natural numbers 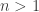 by
by  where
where  is the sum of the divisors of
is the sum of the divisors of  and
and  is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of
is the natural logaritm. We require the properties of extremely abundant numbers, that is to say left to right maxima of  . We also use the colossally abundant and hyper abundant numbers. A number
. We also use the colossally abundant and hyper abundant numbers. A number  is said to be colossally abundant if, for some
is said to be colossally abundant if, for some 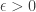 ,
,  for all
for all 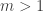 . Let us call hyper abundant an integer
. Let us call hyper abundant an integer  for which there exists
for which there exists  such that
such that  for all
for all 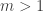 . The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part
. The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part  . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. We state that the Riemann hypothesis is true if and only if there exist infinitely many consecutive colossally abundant numbers  such that
such that  . In addition, we prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers
. In addition, we prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers  with any parameter
with any parameter  .
.
https://easychair.org/publications/preprint_open/b5Wk
Official and not removable last update on new criterion of the Riemann hypothesis!!!
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 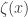 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://easychair.org/publications/preprint_open/rnSr
Official and not removable last update on solution of the Riemann hypothesis!!!
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 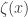 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some  . Since the inequality
. Since the inequality  does not hold for some
does not hold for some  and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://dx.doi.org/10.13140/RG.2.2.25992.70408/3
New update on solution of the Riemann hypothesis!!!
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 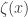 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some 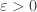 . Since the inequality
. Since the inequality  never holds for every
never holds for every 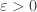 and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://dx.doi.org/10.13140/RG.2.2.25992.70408/4
New possible final update on solution of the Riemann hypothesis!!!
Thanks in advance…
On the nontrivial zeros of the Riemann zeta function
(A Millennium Prize Problem)
The Riemann hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality
. It is considered by many to be the most important unsolved problem in pure mathematics. There are several statements equivalent to the famous Riemann hypothesis. In 2011, Solé and Planat stated that, the Riemann hypothesis is true if and only if the inequality  holds for all
holds for all  , where
, where  is the first Chebyshev function,
is the first Chebyshev function,  is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 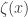 is the Riemann zeta function and
is the Riemann zeta function and  is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers
is the natural logarithm. In this note, using Solé and Planat criterion, we prove that, when the Riemann hypothesis is false, then there are infinitely many natural numbers  for which
for which  could be satisfied for some
could be satisfied for some 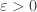 . Since the inequality
. Since the inequality  never holds for every
never holds for every 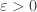 and large enough
and large enough  , then the Riemann hypothesis is true by principle of non-contradiction.
, then the Riemann hypothesis is true by principle of non-contradiction.
https://easychair.org/publications/preprint_open/NzFD
Official and non-removable last update on solution of the Riemann hypothesis!!!
Thanks in advance…
In this notes, we finally introduce new criteria for the Riemann Hypothesis:
(A Millennium Prize Problem)
Riemann Hypothesis on Grönwall’s Function
https://easychair.org/publications/preprint_open/b5Wk
Riemann Hypothesis on Ramanujan’s Function
https://easychair.org/publications/preprint_open/DLJ5
Robin’s Criterion on Superabundant Numbers
https://easychair.org/publications/preprint_open/jC7l
Alicia Nash-“I need to believe that something extraordinary is possible”
Thank You for Letting Me Share…
Finally, we introduce new criteria for the Riemann Hypothesis:
(A Millennium Prize Problem)
Riemann Hypothesis on Grönwall’s Function
https://easychair.org/publications/preprint_open/b5Wk
Riemann Hypothesis on Ramanujan’s Function
https://easychair.org/publications/preprint_open/DLJ5
Robin’s Criterion on Superabundant Numbers
https://easychair.org/publications/preprint_open/jC7l
Alicia Nash-“I need to believe that something extraordinary is possible”
Thank You for Letting Me Share…
The smallest gap between primes
(Twin Prime Conjecture)
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In May 2013, the popular Yitang Zhang’s paper was accepted by the journal Annals of Mathematics where it was announced that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. A few months later, James Maynard gave a different proof of Yitang Zhang’s theorem and showed that there are infinitely many prime gaps with size of at most 600. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://dx.doi.org/10.13140/RG.2.2.19448.93440
The Riemann Hypothesis and Twin Prime Conjecture are close related.
Thank You for Letting Me Share…
The smallest gap between primes
(Twin prime conjecture)
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In May 2013, the popular Yitang Zhang’s paper was accepted by the journal Annals of Mathematics where it was announced that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. A few months later, James Maynard gave a different proof of Yitang Zhang’s theorem and showed that there are infinitely many prime gaps with size of at most 600. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://easychair.org/publications/preprint_open/7gzW
Permanent and non-removable draft link!!!!
The Riemann Hypothesis and Twin prime conjecture are close related.
Thank You for Letting Me Share…
The smallest gap between primes
(Twin prime conjecture)
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In May 2013, the popular Yitang Zhang’s paper was accepted by the journal Annals of Mathematics where it was announced that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. A few months later, James Maynard gave a different proof of Yitang Zhang’s theorem and showed that there are infinitely many prime gaps with size of at most 600. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://dx.doi.org/10.13140/RG.2.2.24010.24003
This is a new update supported by the Experiment findings:
https://dx.doi.org/10.13140/RG.2.2.15621.63200
The Riemann Hypothesis and Twin prime conjecture are close related.
Thank You for Letting Me Share…
Twin Prime Conjecture (Solved):
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In May 2013, the popular Yitang Zhang’s paper was accepted by the journal Annals of Mathematics where it was announced that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. A few months later, James Maynard gave a different proof of Yitang Zhang’s theorem and showed that there are infinitely many prime gaps with size of at most 600. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://dx.doi.org/10.13140/RG.2.2.24010.24003
This is a new update supported by the Experiment findings:
https://dx.doi.org/10.13140/RG.2.2.15621.63200
Thank You for Letting Me Share…
The smallest gap between primes
(Twin prime conjecture)
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In May 2013, the popular Yitang Zhang’s paper was accepted by the journal Annals of Mathematics where it was announced that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. A few months later, James Maynard gave a different proof of Yitang Zhang’s theorem and showed that there are infinitely many prime gaps with size of at most 600. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://easychair.org/publications/preprint_open/pX6T
New update on permanent and non-removable draft link.
Thank You for Letting Me Share…
The smallest gap between primes
(Twin prime conjecture)
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In May 2013, the popular Yitang Zhang’s paper was accepted by the journal Annals of Mathematics where it was announced that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. A few months later, James Maynard gave a different proof of Yitang Zhang’s theorem and showed that there are infinitely many prime gaps with size of at most 600. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://dx.doi.org/10.13140/RG.2.2.29226.90565
We simplify much more the final proof of the Twin prime conjecture.
Thank You for Letting Me Share…
The smallest gap between primes
(Twin prime conjecture)
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In May 2013, the popular Yitang Zhang’s paper was accepted by the journal Annals of Mathematics where it was announced that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. A few months later, James Maynard gave a different proof of Yitang Zhang’s theorem and showed that there are infinitely many prime gaps with size of at most 600. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://easychair.org/publications/preprint_open/m6lV
Final and non-removable link where it was simplified the proof.
Thank You for Letting Me Share…
Yitang Zhang Paper on Riemann is wrong due to the fact that all Zeros lie on Zero line S = -i(pi) /ln(P^2^n )Also Barry Mazur using these number showed the so-called zeros are spectrum of primes !
Note that these roots also were studied by annal of mathematics for 7 months and decided not to publish
Homogeneous Diophantine equation of degree two in NP-complete
In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution. We prove that this decision problem is actually in under the constraint that the each variable is required to be evaluated in
under the constraint that the each variable is required to be evaluated in  .
.
https://dx.doi.org/10.13140/RG.2.2.10132.17281
Thank You for Letting Me Share…
Homogeneous Diophantine equation of degree two in NP-complete
In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution. We prove that this decision problem is actually in \textit{NP–complete} under the constraint that the each variable is required to be evaluated in {0, 1}.
https://dx.doi.org/10.13140/RG.2.2.18520.78087
Thank You for Letting Me Share…
Homogeneous Diophantine equation of degree two in NP-complete
In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution. We prove that this decision problem is actually in under the constraint that the each variable is required to be evaluated in
under the constraint that the each variable is required to be evaluated in  .
.
https://dx.doi.org/10.13140/RG.2.2.12229.32483
Thank You for Letting Me Share…
Homogeneous Diophantine equation of degree two in NP-complete
In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution. We prove that this decision problem is actually in under the constraint that the each variable is required to be evaluated in
under the constraint that the each variable is required to be evaluated in  .
.
https://easychair.org/publications/preprint_open/nWCj
Updated and non-removable link for the draft.
Thank You for Letting Me Share…
Assuming the Birch and Swinnerton-Dyer conjecture, is a congruent number if and only if the number of triplets of integers
is a congruent number if and only if the number of triplets of integers 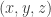 satisfying
satisfying  is twice the number of triplets satisfying
is twice the number of triplets satisfying  . (see Tunnell’s theorem).
. (see Tunnell’s theorem).
Counting solutions of the homogeneous Diophantine equations of degree two seems to be a problem in sharp-P-complete (see my previous posts).
Detecting whether is congruent or not seems to be a problem in NP: congruent numbers could be easily checked by a congruum since every congruent number is a product of a congruum and the square of a rational number.
is congruent or not seems to be a problem in NP: congruent numbers could be easily checked by a congruum since every congruent number is a product of a congruum and the square of a rational number.
Under the assumption that P = NP and P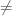 sharp-P, is Birch and Swinnerton-Dyer conjecture indeed false?
sharp-P, is Birch and Swinnerton-Dyer conjecture indeed false?
Sharp-P and the Birch and Swinnerton-Dyer conjecture
Assuming the Birch and Swinnerton-Dyer conjecture, an odd square-free integer is a congruent number if and only if the number of triplets of integers
is a congruent number if and only if the number of triplets of integers 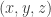 satisfying
satisfying  is twice the number of triplets satisfying
is twice the number of triplets satisfying  due to Tunnell’s theorem. However, we show these equations are instances of a variant of counting solutions of the homogeneous Diophantine equations of degree two which is a
due to Tunnell’s theorem. However, we show these equations are instances of a variant of counting solutions of the homogeneous Diophantine equations of degree two which is a  problem. Deciding whether
problem. Deciding whether  is congruent or not is a problem in
is congruent or not is a problem in  since congruent numbers could be easily checked by a congruum, because of every congruent number is a product of a congruum and the square of a rational number. We conjecture that if
since congruent numbers could be easily checked by a congruum, because of every congruent number is a product of a congruum and the square of a rational number. We conjecture that if  and
and  , then the Birch and Swinnerton-Dyer conjecture would be false.
, then the Birch and Swinnerton-Dyer conjecture would be false.
https://www.researchgate.net/publication/365733789_Sharp-P_and_the_Birch_and_Swinnerton-Dyer_conjecture
Thank You for Letting Me Share…
Sharp-P and the Birch and Swinnerton-Dyer conjecture
Assuming the Birch and Swinnerton-Dyer conjecture, an odd square-free integer is a congruent number if and only if the number of triplets of integers
is a congruent number if and only if the number of triplets of integers  satisfying
satisfying  is twice the number of triplets satisfying
is twice the number of triplets satisfying  due to Tunnell’s theorem. However, we show these equations are instances of a variant of counting solutions of the homogeneous Diophantine equations of degree two which is a
due to Tunnell’s theorem. However, we show these equations are instances of a variant of counting solutions of the homogeneous Diophantine equations of degree two which is a  problem. Deciding whether
problem. Deciding whether  is congruent or not is a problem in
is congruent or not is a problem in  since congruent numbers could be easily checked by a congruum, because of every congruent number is a product of a congruum and the square of a rational number. We conjecture that if
since congruent numbers could be easily checked by a congruum, because of every congruent number is a product of a congruum and the square of a rational number. We conjecture that if  and
and  , then the Birch and Swinnerton-Dyer conjecture would be false.
, then the Birch and Swinnerton-Dyer conjecture would be false.
https://easychair.org/publications/preprint_open/hqbw
Non-removable link of the draft.
Thank You for Letting Me Share…
Between October 24 – November 25, 2022 (1 month), I have done:
(Two manuscripts about the Millennium Problem: Riemann Hypothesis):
https://easychair.org/publications/preprint_open/b5Wk
https://easychair.org/publications/preprint_open/jC7l
(A manuscript about a Hilbert’s Problem: The Twin Prime Conjecture):
https://easychair.org/publications/preprint_open/m6lV
(Another manuscript about a Millennium Problem: P vs NP):
https://easychair.org/publications/preprint_open/nWCj
(Another manuscript about a Millennium Problem: The Birch and Swinnerton-Dyer Conjecture):
https://easychair.org/publications/preprint_open/hqbw
Time to take a break!!!
Between October 24 – November 25, 2022 (1 month):
(Two manuscripts about the Millennium Problem: Riemann Hypothesis):
https://easychair.org/publications/preprint_open/b5Wk
https://easychair.org/publications/preprint_open/jC7l
(A manuscript about a Hilbert’s Problem: The Twin Prime Conjecture):
https://easychair.org/publications/preprint_open/m6lV
(Another manuscript about a Millennium Problem: P vs NP):
https://easychair.org/publications/preprint_open/nWCj
(Another manuscript about a Millennium Problem: The Birch and Swinnerton-Dyer Conjecture):
https://easychair.org/publications/preprint_open/hqbw
Between October 24 – November 25, 2022:
(Two manuscripts about the Millennium Problem: Riemann Hypothesis):
https://easychair.org/publications/preprint_open/b5Wk
https://easychair.org/publications/preprint_open/jC7l
(A manuscript about a Hilbert’s Problem: The Twin Prime Conjecture):
https://easychair.org/publications/preprint_open/m6lV
(Another manuscript about a Millennium Problem: P vs NP):
https://easychair.org/publications/preprint_open/nWCj
(Another manuscript about a Millennium Problem: The Birch and Swinnerton-Dyer Conjecture):
https://easychair.org/publications/preprint_open/hqbw
Fixed a small detail (but important) in definition of problem BHDE (previously problem MHDE). My intention is to create a link between these two unsolved problems (FP vs Sharp-P and the Birch and Swinnerton-Dyer conjecture), but I did it in form of conjecture in order to others could develop it (trying to do it in the same way Gerhard Frey did it for Fermat’s Last Theorem in 1984).
https://dx.doi.org/10.13140/RG.2.2.35573.24809
Thank You for Letting Me Share…
We conjecture that if and
and  , then the Birch and Swinnerton-Dyer conjecture would be false. My intention is to create a link between these two unsolved problems (
, then the Birch and Swinnerton-Dyer conjecture would be false. My intention is to create a link between these two unsolved problems ( and the Birch and Swinnerton-Dyer conjecture), but I did it in form of conjecture in order to others could develop it (trying to do it in the same way Gerhard Frey did it for Fermat’s Last Theorem in 1984).
and the Birch and Swinnerton-Dyer conjecture), but I did it in form of conjecture in order to others could develop it (trying to do it in the same way Gerhard Frey did it for Fermat’s Last Theorem in 1984).
https://easychair.org/publications/preprint_open/5WlL
Last update and non-removable link for the draft.
Thank You for Letting Me Share…
#math #science #go #work
Between October 24 – November 26, 2022 (I have called “my golden month”):
(Two manuscripts about the Millennium Problem: Riemann Hypothesis):
Riemann Hypothesis on Grönwall’s Function
https://easychair.org/publications/preprint_open/b5Wk
Robin’s Criterion on Superabundant Numbers
https://easychair.org/publications/preprint_open/jC7l
(A manuscript about a Hilbert’s Problem: The Twin Prime Conjecture):
The Smallest Gap Between Primes
https://easychair.org/publications/preprint_open/m6lV
(Another manuscript about a Millennium Problem: P vs NP):
Homogeneous Diophantine Equation of Degree Two in NP-Complete
https://easychair.org/publications/preprint_open/nWCj
(Another manuscript about a Millennium Problem: The Birch and Swinnerton-Dyer Conjecture):
Sharp-P and the Birch and Swinnerton-Dyer Conjecture
https://easychair.org/publications/preprint_open/5WlL
I believe I’m making progress (I hope so…)
Thank You for Letting Me Share…
“My golden month”:
(Two manuscripts about the Millennium Problem: Riemann Hypothesis):
Riemann Hypothesis on Grönwall’s Function
https://easychair.org/publications/preprint_open/b5Wk
Robin’s Criterion on Superabundant Numbers
https://easychair.org/publications/preprint_open/jC7l
(A manuscript about a Hilbert’s Problem: The Twin Prime Conjecture):
The Smallest Gap Between Primes
https://easychair.org/publications/preprint_open/m6lV
(Another manuscript about a Millennium Problem: P vs NP):
Homogeneous Diophantine Equation of Degree Two in NP-Complete
https://easychair.org/publications/preprint_open/nWCj
(Another manuscript about a Millennium Problem: The Birch and Swinnerton-Dyer Conjecture):
Sharp-P and the Birch and Swinnerton-Dyer Conjecture
https://easychair.org/publications/preprint_open/5WlL
Thank You for Letting Me Share…
Sharp-P and the Birch and Swinnerton-Dyer conjecture
Assuming the Birch and Swinnerton-Dyer conjecture, an odd square-free integer is a congruent number if and only if the number of triplets of integers
is a congruent number if and only if the number of triplets of integers 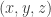 satisfying
satisfying  is twice the number of triplets satisfying
is twice the number of triplets satisfying  due to Tunnell’s theorem. However, we show these equations are instances of a variant of counting solutions of the homogeneous Diophantine equations of degree two which is a
due to Tunnell’s theorem. However, we show these equations are instances of a variant of counting solutions of the homogeneous Diophantine equations of degree two which is a  problem. Deciding whether
problem. Deciding whether  is congruent or not is a problem in
is congruent or not is a problem in  since congruent numbers could be easily checked by a congruum, because of every congruent number is a product of a congruum and the square of a rational number. Certainly, every congruum is in the form of
since congruent numbers could be easily checked by a congruum, because of every congruent number is a product of a congruum and the square of a rational number. Certainly, every congruum is in the form of  (with
(with 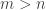 ), where
), where  and
and  are two distinct positive integers. We conjecture that if
are two distinct positive integers. We conjecture that if  and
and  , then the Birch and Swinnerton-Dyer conjecture would be false.
, then the Birch and Swinnerton-Dyer conjecture would be false.
https://easychair.org/publications/preprint_open/3v94
Final update and non-removable link for the draft.
Thank You for Letting Me Share…
We show the impossible is possible:
Riemann Hypothesis:
https://easychair.org/publications/preprint_open/b5Wk
Twin Prime Conjecture:
https://easychair.org/publications/preprint_open/m6lV
Robin’s Criterion:
https://easychair.org/publications/preprint_open/jC7l
Alicia Nash-“I need to believe that something extraordinary is possible”
Thank You for Letting Me Share…
Finally, we show the impossible is possible:
Riemann Hypothesis:
https://easychair.org/publications/preprint_open/b5Wk
Twin Prime Conjecture:
https://easychair.org/publications/preprint_open/m6lV
Robin’s Criterion:
https://easychair.org/publications/preprint_open/jC7l
Alicia Nash-“I need to believe that something extraordinary is possible”
We made progress on Riemann Hypothesis and Twin Prime Conjecture:
(A Millennium Prize Problem)
(Two Hilbert’s Problems)
Riemann Hypothesis on Grönwall’s Function
https://easychair.org/publications/preprint_open/b5Wk
The Smallest Gap Between Primes
https://easychair.org/publications/preprint_open/m6lV
Robin’s Criterion on Superabundant Numbers
https://easychair.org/publications/preprint_open/jC7l
Homogeneous Diophantine Equation of Degree Two in NP-Complete
In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution: we are able to reject an instance when there is no solution reducing the equation modulo p. We prove that this decision problem is actually in NP-complete under the constraints that all solutions contain only positive integers which are actually a residue of modulo a single positive integer. This problem remains in NP-complete even when all the coefficients are non-negative.
https://easychair.org/publications/preprint_open/J1P2
Final update and non-removable link for the draft.
Thank You for Letting Me Share…
Note on the Riemann Hypothesis: International Conference on Recent Developments in Mathematics (ICRDM 2022)
The Riemann Hypothesis is a conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. In 1984, Guy Robin stated a new criterion for the Riemann Hypothesis. We prove the Riemann Hypothesis is true using the Robin’s criterion.
https://dx.doi.org/10.13140/RG.2.2.27155.35369
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
Goldbach’s conjecture is one of the most difficult unsolved problems in mathematics. This states that every even natural number greater than 2 is the sum of two prime numbers. In 1973, Chen Jingrun proved that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes). In 2015, Tomohiro Yamada, using the Chen’s theorem, showed that every even number can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer
can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer  is equal to
is equal to  , where
, where  is an almost prime with at most two prime factors and
is an almost prime with at most two prime factors and  is a prime number. In this note, we prove that for every even number
is a prime number. In this note, we prove that for every even number  , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  and
and  means "much greater than''. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
means "much greater than''. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://dx.doi.org/10.13140/RG.2.2.34501.73445
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
Goldbach’s conjecture is one of the most difficult unsolved problems in mathematics. This states that every even natural number greater than 2 is the sum of two prime numbers. In 1973, Chen Jingrun proved that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes). In 2015, Tomohiro Yamada, using the Chen’s theorem, showed that every even number can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer
can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer  is equal to
is equal to  , where
, where  is an almost prime with at most two prime factors and
is an almost prime with at most two prime factors and  is a prime number. In this note, we prove that for every even number
is a prime number. In this note, we prove that for every even number  , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  and
and  means "much greater than''. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
means "much greater than''. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://easychair.org/publications/preprint_open/gH9d
A non-removable draft.
https://easychair.org/publications/preprint_open/gH9d
In this note, we prove that for every even number , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  is the sum-of-divisors function of
is the sum-of-divisors function of  ,
,  and
and  means "much greater than''.
means "much greater than''.
https://easychair.org/publications/preprint_open/gH9d
Thank You for Letting Me Share…
P versus NP is considered as one of the most important open problems in computer science. This consists in knowing the answer of the following question: Is P equal to NP? It was essentially mentioned in 1955 from a letter written by John Nash to the United States National Security Agency. However, a precise statement of the P versus NP problem was introduced independently by Stephen Cook and Leonid Levin. Since that date, all efforts to find a proof for this problem have failed. In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution: we are capable to reject an instance when there is no solution reducing the equation modulo p. We prove that this decision problem is actually in NP-complete under the constraints that all solutions contain only positive integers which are actually residues of modulo a single positive integer.
https://dx.doi.org/10.13140/RG.2.2.17639.32168
Thank You for Letting Me Share…
Homogeneous Diophantine equation of degree two in NP-complete
P versus NP is considered as one of the most important open problems in computer science. This consists in knowing the answer of the following question: Is P equal to NP? It was essentially mentioned in 1955 from a letter written by John Nash to the United States National Security Agency. However, a precise statement of the P versus NP problem was introduced independently by Stephen Cook and Leonid Levin. Since that date, all efforts to find a proof for this problem have failed. In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution: we are capable to reject an instance when there is no solution reducing the equation modulo p. We prove that this decision problem is actually in NP-complete under the constraints that all solutions contain only positive integers which are actually residues of modulo a single positive integer.
https://easychair.org/publications/preprint_open/sTlm
Non-removable draft.
Thank You for Letting Me Share…
This is a release of the binaries of a project which solves an instance of the problem 3SAT in where n is the number of variables and m is the number of clauses. The exponent in the algorithm is not very good, so this release would be only feasible for small values of n.
where n is the number of variables and m is the number of clauses. The exponent in the algorithm is not very good, so this release would be only feasible for small values of n.
The original Boolean formula is translated to a homogeneous polynomial of degree 2. Finally, we solve it using dynamic programming based on the implementation of the problem Subset Sum. The reduction is simplified in order to obtain efficiency. Mutable objects need to be changed.
Note that, the problem could be solved by the Hasse-Minkowski theorem. We know the solution on dynamic programming of the problem Subset Sum could be exponential. However, in our polynomial time reduction the problem remains polynomial over the number of variables.
https://github.com/frankvegadelgado/sat/releases/tag/initial
Thank You for Letting Me Share…
P versus NP is considered as one of the most important open problems in computer science. This consists in knowing the answer of the following question: Is P equal to NP? It was essentially mentioned in 1955 from a letter written by John Nash to the United States National Security Agency. However, a precise statement of the P versus NP problem was introduced independently by Stephen Cook and Leonid Levin. Since that date, all efforts to find a proof for this problem have failed. In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution: we are capable to reject an instance when there is no solution reducing the equation modulo p. We reduce the NP-complete problem 3SAT to a homogeneous Diophantine equation of degree 2 in polynomial time. This is is solvable modulo 2 if and only if the Boolean formula is satisfiable. Note that, we can generate all possible integer solutions starting for a single non-trivial solution.
https://github.com/frankvegadelgado/sat/releases/tag/initial
Thank You for Letting Me Share…
P versus NP is considered as one of the most important open problems in computer science. This consists in knowing the answer of the following question: Is P equal to NP? It was essentially mentioned in 1955 from a letter written by John Nash to the United States National Security Agency. However, a precise statement of the P versus NP problem was introduced independently by Stephen Cook and Leonid Levin. Since that date, all efforts to find a proof for this problem have failed.
Directed Hamiltonian Path
Instance: A directed graph G = (V, E) of n vertices, such that each vertex is labeled with a unique integer from 1 to n. A Hamiltonian path is a simple path (with no repeated nodes) such that this one contains all the vertices in V.
Question: Is there a Hamiltonian path from 1 to n in the graph G?
Note: This problem is NP-complete.
We solve this problem in polynomial time in order . If there is any NP-complete solvable in polynomial time, then P = NP.
. If there is any NP-complete solvable in polynomial time, then P = NP.
We based our algorithm on this property of the Euler–Mascheroni constant:
where is the Harmonic series until n,
is the Harmonic series until n,  is the Euler–Mascheroni constant and
is the Euler–Mascheroni constant and  which approaches 0 as n goes to infinity. Note that, we use the first 170000 digits of
which approaches 0 as n goes to infinity. Note that, we use the first 170000 digits of  , so this could fail for n large enough (However, Seungmin Kim & Ian Cutress found the first 600000000100 digits on May 26, 2020).
, so this could fail for n large enough (However, Seungmin Kim & Ian Cutress found the first 600000000100 digits on May 26, 2020).
https://github.com/frankvegadelgado/hamiltonian/releases/tag/executable
Scala code by Frank Vega
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
Goldbach’s conjecture is one of the most difficult unsolved problems in mathematics. This states that every even natural number greater than 2 is the sum of two prime numbers. In 1973, Chen Jingrun proved that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes). In 2015, Tomohiro Yamada, using the Chen’s theorem, showed that every even number can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer
can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer  is equal to
is equal to  , where
, where  is an almost prime with at most two prime factors and
is an almost prime with at most two prime factors and  is a prime number. In this note, we prove that for every even number
is a prime number. In this note, we prove that for every even number  , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  and
and  is the sum-of-divisors function of
is the sum-of-divisors function of  . Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://dx.doi.org/10.13140/RG.2.2.20508.16004
Thank You for Letting Me Share…
Homogeneous Diophantine equation of degree two in NP-complete
We prove the following problem is NP-complete (in a trivial way):
“Decide whether a homogeneous Diophantine equations of degree two has integer solutions which are actually residues of modulo a single positive integer.”
However, homogeneous Diophantine equations of degree two are considered easier to solve. Certainly, using the Hasse principle we may able to decide whether a homogeneous Diophantine equation of degree two has an integer solution: we are capable to reject an instance when there is no solution reducing the equation modulo p.
In this way, we prove that this problem is also in coNP since the previous mentioned prime p can be polynomially bounded by the instance and checking whether an assignment is not a solution can be done in polynomial time.
Consequently, we show that NP = coNP in a trivial way since any NP-complete problem in coNP is pretty enough evidence for this result.
https://dx.doi.org/10.13140/RG.2.2.17639.32168
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
In this note, we prove that for every even number , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  and
and  is the sum-of-divisors function of
is the sum-of-divisors function of  .
.
https://dx.doi.org/10.13140/RG.2.2.16313.85603
Thank You for Letting Me Share…
Homogeneous Diophantine equation of degree two in NP-complete
Extended comments (specifically for you in case you might like to go deep):
The Hasse principle guarantee if there is a rational solution, then there are solutions modulo every prime p. In this way, if there is no solution reducing the equation modulo some prime p, then the equation has not a rational solution. There is a trivial mechanism for transforming rational solutions to integer solutions residues some prime, so there are not integer solutions when there is no solution reducing the equation modulo for some prime p. I have realized that this disqualification (the equivalent string to a certificate but in coNP) prime p tends to be bounded by the coefficients of the equation and checking whether
the equation has not a p-adic solution could be solved in polynomial time. The existence of this disqualification for every homogeneous Diophantine equations of degree two which has not integer solution makes this NP-complete problem in coNP (this implies that NP = coNP). This is a very short and clean result:
https://dx.doi.org/10.13140/RG.2.2.17639.32168
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
In this note, we prove that for every even number , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  ,
,  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the natural logarithm. That is also true whenever
is the natural logarithm. That is also true whenever  based on the previously defined prime
based on the previously defined prime  .
.
https://dx.doi.org/10.13140/RG.2.2.16576.00001
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
We prove that for every even number , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  ,
,  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the natural logarithm.
is the natural logarithm.
https://dx.doi.org/10.13140/RG.2.2.16890.57280
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
Goldbach’s conjecture is one of the most difficult unsolved problems in mathematics. This states that every even natural number greater than 2 is the sum of two prime numbers. In 1973, Chen Jingrun proved that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes). In 2015, Tomohiro Yamada, using the Chen’s theorem, showed that every even number can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer
can be represented as the sum of a prime and a product of at most two primes. In 2002, Ying Chun Cai proved that every sufficiently large even integer  is equal to
is equal to  , where
, where 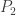 is an almost prime with at most two prime factors and
is an almost prime with at most two prime factors and  is a prime number. In this note, we prove that for every even number
is a prime number. In this note, we prove that for every even number  , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  ,
,  is the sum-of-divisors function of
is the sum-of-divisors function of  and
and  is the natural logarithm. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
is the natural logarithm. Indeed, this is a trivial and short note very easy to check and understand which is a breakthrough result at the same time.
https://dx.doi.org/10.13140/RG.2.2.25279.18084
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
We prove that for every even number , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  and
and  is the sum-of-divisors function of
is the sum-of-divisors function of  .
.
https://dx.doi.org/10.13140/RG.2.2.14373.99046
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
The Goldbach’s conjecture has been verified for every even number . In this note, we prove that for every even number
. In this note, we prove that for every even number  , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  and
and  is the sum-of-divisors function of
is the sum-of-divisors function of  .
.
https://dx.doi.org/10.13140/RG.2.2.36263.01447
Thank You for Letting Me Share…
L versus NP
Many computer scientists believe that the problem L versus NP is easier to solve than P versus NP. However, we prove that L = NL if and only if L = NP. In this way, we conclude that a proof for a separation of the complexity classes L and NP is so hard to find as proving that L is not equal to NL.
https://dx.doi.org/10.13140/RG.2.2.34385.40801
Thank You for Letting Me Share…
Riemann Hypothesis on Grönwall’s Function
We prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers n with any parameter u ⪆ 1. We claim that there could be infinitely many hyper abundant numbers with any parameter u ⪆ 1.
https://easychair.org/publications/preprint_open/mWfm
Thank You for Letting Me Share…
The Smallest Gap Between Primes
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. This conjecture has been one of the great open problems in number theory for many years. In this note, using arithmetic operations, we prove that the twin prime conjecture is true.
https://easychair.org/publications/preprint_open/s2RH
Thank You for Letting Me Share…
The Smallest Gap Between Primes
A prime gap is the difference between two successive prime numbers. Two is the smallest possible gap between primes. A twin prime is a prime that has a prime gap of two. The twin prime conjecture states that there are infinitely many twin primes. A collaborative effort in the Polymath Project, led by Terence Tao, reduced to the lower bound 246 just using Zhang and Maynard results as the main theoretical background. In this note, using arithmetic operations, we prove that the twin prime conjecture is true. This conjecture has been one of the great open problems in number theory for many years.
https://easychair.org/publications/preprint_open/4W7v
Thank You for Letting Me Share…
NP on Logarithmic Space
P versus NP is considered as one of the most important open problems in computer science. Whether L = NL is another fundamental question that it is as important as it is unresolved. We prove the breakthrough result that L = NL. Besides, we show that every NP problem is in L with oracle access to L.
https://dx.doi.org/10.13140/RG.2.2.20105.11367
Thank You for Letting Me Share…
NP on Logarithmic Space
The P versus NP problem is considered as one of the most important open problems in computer science. Whether L = NL is another fundamental question that it is as important as it is unresolved. We prove the breakthrough result that L = NL. Besides, we show that every NP problem is in L with oracle access to L.
https://easychair.org/publications/preprint_open/s7S7
This is the last and non-removable version that is ready for peer review…
Thank You for Letting Me Share…
NP on Logarithmic Space
The P versus NP problem is a major unsolved problem in theoretical computer science. Another major complexity classes are L and NL. Whether L = NL is another fundamental question that it is as important as it is unresolved. We prove the breakthrough result that L = NL. Besides, we show that every NP problem is in L with oracle access to L.
https://easychair.org/publications/preprint_open/RhwV
This version was sent for peer-review…
Thank You for Letting Me Share…
NP on Logarithmic Space
Whether L = NL is a fundamental question that it is as important as it is unresolved. We prove the breakthrough result that L = NL. Besides, we show that every NP problem is in L with oracle access to L.
https://dx.doi.org/10.13140/RG.2.2.20105.11367
I have to do a replacement since I needed to check for two vertices v and w in a independent set whether the edges (v, w) and (w, v) do not exist at the same time (we only checked the edge (v, w) in previous version) since the graph is a directed graph (digraph).
Thank You for Letting Me Share…
Deep on Goldbach’s conjecture
Goldbach’s conjecture is one of the most difficult unsolved problems in mathematics. This states that every even natural number greater than 2 is the sum of two prime numbers. The Goldbach’s conjecture has been verified for every even number . In this note, we prove that for every even number
. In this note, we prove that for every even number  , if there is a prime
, if there is a prime  and a natural number
and a natural number  such that
such that  ,
,  ,
,  and
and  is coprime with
is coprime with  , then
, then  is necessarily a prime number when
is necessarily a prime number when  and
and  is the sum-of-divisors function of
is the sum-of-divisors function of  . The previous inequality
. The previous inequality  holds whenever
holds whenever  also holds and
also holds and  is an odd number, where
is an odd number, where  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the natural logarithm. This implies that the Goldbach's conjecture is true when the Riemann hypothesis is true.
is the natural logarithm. This implies that the Goldbach's conjecture is true when the Riemann hypothesis is true.
https://dx.doi.org/10.13140/RG.2.2.13146.41925
Thank You for Letting Me Share…
They [formulae 1.10 – 1.12 of Ramanujan] must be true because, if they were not true, no one would have had the imagination to invent them. G. H. Hardy.
I tried to make progress into the following approaches:
Twin prime conjecture: https://www.researchgate.net/publication/365424918_The_smallest_gap_between_primes
P vs NP and L vs NL: https://www.researchgate.net/publication/366953923_NP_on_Logarithmic_Space
and finally
Goldbach’s conjecture: https://www.researchgate.net/publication/367150776_Deep_on_Goldbach%27s_conjecture
Note also that, I tried to introduce two distinct possible proofs for the Riemann Hypothesis:
https://www.researchgate.net/publication/364474757_Riemann_Hypothesis_on_Gronwall%27s_Function
https://www.researchgate.net/publication/365131766_Robin%27s_criterion_on_superabundant_numbers
It was only with Hardy’s help that Ramanujan became the scholar we know him as today: it wouldn’t probably exist Ramanujan’s contribution without his help.
Thank You for Letting Me Share…
My current contribution:
Twin prime conjecture: https://dx.doi.org/10.13140/RG.2.2.29226.90565
L versus NP: https://dx.doi.org/10.13140/RG.2.2.20105.11367
Goldbach’s conjecture: https://dx.doi.org/10.13140/RG.2.2.13146.41925
Riemann Hypothesis (I): https://dx.doi.org/10.13140/RG.2.2.22658.56002
Riemann Hypothesis (II): https://dx.doi.org/10.13140/RG.2.2.23731.71200
Thank You for Letting Me Share…
Frequently, people push you to find a practical applications for any of your pure mathematical drafts and in most cases those interactions become positive.
That is the case of my recent approach on the Goldbach’s conjecture:
https://dx.doi.org/10.13140/RG.2.2.13146.41925
It is better to give a naive explanation to reach more curious audience about it:
Suppose that some teenager argue that 11 is not prime and my paper got published. Then, you only have to convince him that 29 is prime and 40 is an even number. After that, you only have to show him that
40 / (1.7811 * 11 * ln(ln(11))) + 20^(0.889) + 1 + (11 – 1) / 2 ≈ 22 ≥ 20
since your opponent truly believes that my paper is correct. Of course, I proved this only for all even numbers N ≥ 410^(18). Certainly, this comment has only an educative goal and does not pretend to be a rigorous math evidence (40 is much lesser than 410^(18)).
I suspect that this result could be extended for a wide range of even numbers lesser than 4*10^(18). For that reason, I decided to answer people’s question with simple even numbers such as 40. However, my intuition requires another paper maybe more difficult than this one or a feasible computer validation.
However, in case of being correct this can be applied for finding large prime numbers with a lower computational cost. For example, we can start the search from a well-known and large Mersenne prime and find more large prime numbers relative close to this big number using a very feasible time complexity.
Thank You for Letting Me Share…
They [formulae 1.10–1.12 of Ramanujan] must be true because, if they were not true, no one would have had the imagination to invent them. G. H. Hardy.
Twin prime conjecture:
https://dx.doi.org/10.13140/RG.2.2.29226.90565
L versus NP:
https://dx.doi.org/10.13140/RG.2.2.20105.11367
Riemann Hypothesis (on hyper abundant numbers):
https://dx.doi.org/10.13140/RG.2.2.22658.56002
Riemann Hypothesis (on Robin’s criterion):
https://dx.doi.org/10.13140/RG.2.2.23731.71200
It wouldn’t probably exist Ramanujan’s contribution without Hardy’s help.
Homogeneous Diophantine equation of degree two in NP-complete
We say that a quadratic form f has a solution over a field K if this is a homogeneous degree-2 polynomial with coefficients in K and the values of the solution are in K. The theorem Hasse-Minkowski states that a quadratic form f has a solution over Q if and only if f has solution over R and Qp for all primes p. In a quadratic form, we can transform rational solutions into integer solutions. Based on this known result, we could consider that the problem of deciding whether a quadratic form has a solution over Z is a coNP problem. Certainly, using the Hasse principle we may able to reject an instance when there is no solution reducing the equation modulo p. However, we show that the problem of deciding whether a quadratic form has a solution over Zn for a single natural number n is indeed in NP-complete: any NP-complete in coNP implies that NP=coNP. Perhaps, this manuscript can help us in reveal more properties in details about the P vs NP problem.
https://dx.doi.org/10.13140/RG.2.2.10715.03360
Thank You for Letting Me Share…
I hope the following statements could help to move beyond the current frontiers on the smallest gap prime in probably a similar way it did the Zhang and Maynard results:
For all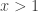 and
and  , we define the function:
, we define the function:
We have is lesser than 0 and
is lesser than 0 and  is greater than 0 for large enough
is greater than 0 for large enough  based on finding their roots using fast computation using the web site WolframAlpha which is an answer engine developed by Wolfram Research. We show that
based on finding their roots using fast computation using the web site WolframAlpha which is an answer engine developed by Wolfram Research. We show that
under the assumption that the Twin Prime Conjecture is false for a large enough nth prime . Hence, by Reductio ad absurdum, the Twin Prime Conjecture is true.
. Hence, by Reductio ad absurdum, the Twin Prime Conjecture is true.
https://dx.doi.org/10.13140/RG.2.2.29226.90565
Previous comment pretty latex formatted:
For all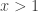 and
and  , we define the function:
, we define the function:
We have is lesser than
is lesser than  and
and  is greater than
is greater than  for large enough
for large enough  based on finding their roots using fast computation using the web site WolframAlpha which is an answer engine developed by Wolfram Research. We show that
based on finding their roots using fast computation using the web site WolframAlpha which is an answer engine developed by Wolfram Research. We show that
under the assumption that the Twin Prime Conjecture is false for a large enough nth prime . Hence, by Reductio ad absurdum, the Twin Prime Conjecture is true.
. Hence, by Reductio ad absurdum, the Twin Prime Conjecture is true.
https://dx.doi.org/10.13140/RG.2.2.29226.90565
The versus
versus  problem:
problem:
We show that the problem of deciding whether a homogeneous Diophantine equations of degree 2 has a solution residues of modulo a single positive integer is in . There are libraries that can solve homogeneous Diophantine equations of degree 2. For example, in Python, you can use the “pely” library to solve homogeneous Diophantine equations of degree 2.
. There are libraries that can solve homogeneous Diophantine equations of degree 2. For example, in Python, you can use the “pely” library to solve homogeneous Diophantine equations of degree 2.
“A city that is set on a hill cannot be hid.” (Matthew 5:14)
https://dx.doi.org/10.13140/RG.2.2.17992.80640
We show the in the problem of deciding whether a homogeneous Diophantine equations of degree 2 has a solution residues of modulo a single positive integer. We could transform this algorithm to an optimization problem that is algorithmically practical solving P-Selective Sets on
in the problem of deciding whether a homogeneous Diophantine equations of degree 2 has a solution residues of modulo a single positive integer. We could transform this algorithm to an optimization problem that is algorithmically practical solving P-Selective Sets on 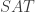 instances that works better when both formulas have approximately the same number of variables and clauses. The whole algorithm is based on the problem of quadratic optimization without constraints which is feasible when we do not restrict the variables to be integers. Certainly, the conversion of a clause
instances that works better when both formulas have approximately the same number of variables and clauses. The whole algorithm is based on the problem of quadratic optimization without constraints which is feasible when we do not restrict the variables to be integers. Certainly, the conversion of a clause  into a small piece of Homogeneous Diophantine Polynomial of degree two on residues of modulo 2
into a small piece of Homogeneous Diophantine Polynomial of degree two on residues of modulo 2
works for integers and real values
and real values  and
and  at the same time, since the expression
at the same time, since the expression  is maximized to the optimal value of
is maximized to the optimal value of  only on solutions in
only on solutions in 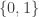 for both cases according to our described and explained reduction. We implement a software solution to this problem, specifically dealing with the problem
for both cases according to our described and explained reduction. We implement a software solution to this problem, specifically dealing with the problem  , that runs feasible using the algorithm PRAXIS (PRincipal AXIS): PRAXIS is a gradient-free local optimization via the “principal-axis method” of Richard Brent. The whole project was developed by the author and it is available in GitHub on MIT License:
, that runs feasible using the algorithm PRAXIS (PRincipal AXIS): PRAXIS is a gradient-free local optimization via the “principal-axis method” of Richard Brent. The whole project was developed by the author and it is available in GitHub on MIT License:
https://frankvegadelgado.github.io/sat/
Indeed, I reduced SAT to solve a polynomial Diophantine equation of degree 2 (homogeneous). I submitted to a conference and a journal and obtained the same response: “it’s cute, but we don’t see any practical application”. Then, I realized that my polynomial time reduction works not only for integers but for real numbers as well. At the end, I noticed that SAT is equivalent to obtain the maximum value of polynomial of degree two. I tried to implement it, but global optimization is not very feasible for quadratic polynomials, so I changed it to local optimization and felt happy with the results.
This the theoretical background which supported such previous implementation:
https://dx.doi.org/10.13140/RG.2.2.36442.82881
Break-SAT2023Testing-by-Capablanca-SAT-Solver-on-March-2023
SAT Competition 2023 is a competitive event for solvers of the Boolean Satisfiability (SAT) problem. They put a few testing instances which people can use to test their solvers. The solvers will be executed with a time limit of 5000 seconds and memory limit of 128GB. We use an alpha version of our SAT solver Capablanca which is much more efficient than the competition’s limits.
https://dx.doi.org/10.13140/RG.2.2.16358.50242
SAT2023Testing-by-SAT-Solver-Capablanca
SAT Competition 2023 is a competitive event for solvers of the Boolean Satisfiability (SAT) problem. They put a few testing instances which people can use to test their solvers. The solvers will be executed within a time limit of 5000 seconds and memory limit of 128GB. We developed our SAT Solver Capablanca which broke all the competition’s limits in time and memory.
https://dx.doi.org/10.13140/RG.2.2.23986.89281
SAT Competition 2023 is a competitive event for solvers of the Boolean Satisfiability (SAT) problem. They put up some test instances that people can use to test their solvers. The solvers will run within a time limit of 5000 seconds and a memory limit of 128 GB. We developed our SAT Solver Capablanca that broke all the limits of the competition in time and memory:
https://www.starexec.org/starexec/secure/details/job.jsp?anonId=0c1f4398-0027-4266-b89a-4fea91d4704c
SAT-Solver-Capablanca
SAT Competition 2023 is a competitive event for solvers of the Boolean Satisfiability (SAT) problem. They put up some test instances that people can use to test their solvers. The solvers will run within a time limit of 5000 seconds and a memory limit of 128 GB. We developed our SAT Solver Capablanca that run under the limits of the competition in time over those testing instances:
https://www.starexec.org/starexec/secure/details/job.jsp?anonId=7eb333e5-2aeb-4214-abc9-41e7eecfe0e5
I invite you to publicly review my paper:
https://www.qeios.com/read/QCDN1G
SAT is as hard as solving Homogeneous Diophantine Equation of Degree Two
P versus NP is considered as one of the most important open problems in computer science. This consists in knowing the answer of the following question: Is P equal to NP? It was essentially mentioned in 1955 from a letter written by John Nash to the United States National Security Agency. However, a precise statement of the P versus NP problem was introduced independently by Stephen Cook and Leonid Levin. Since that date, all efforts to find a proof for this problem have failed. In mathematics, a Diophantine equation is a polynomial equation, usually involving two or more unknowns, such that the only solutions of interest are the integer ones. A homogeneous Diophantine equation is a Diophantine equation that is defined by a homogeneous polynomial. Solving a homogeneous Diophantine equation is generally a very difficult problem. However, homogeneous Diophantine equations of degree two are considered easier to solve. We prove that this decision problem is actually in NP-complete under the constraints that all solutions contain only positive integers which are actually residues of modulo a single positive integer.
Thanks in advance….
This paper has been accepted by two reviewers in a prestigious journal of pure mathematics. The first reviewer accepted on December 4th and the other on April 10th. This works proves the Riemann Hypothesis.
https://www.researchgate.net/publication/364474757_Riemann_Hypothesis_on_Gronwall%27s_Function/figures?lo=1
#mathematics #numbers #primes #research #researchgate #breakthrough
https://www.linkedin.com/pulse/twin-prime-conjecture-frank-vega/
The twin prime conjecture appeared to be invincible through the years. Top mathematicians like Hardy and his colleague Littlewood, among others, couldn’t beat it during their whole career. Nevertheless, they achieved substantial advances that made the conjecture more famous and more tempted to prove. Even Erdős himself, famous for solving difficult problems, was engaged in solving this conjecture. This conjecture states that there are infinitely many primes separated by a gap of 2: for example, 3 and 5, 5 and 7, 11 and 13, etc. In ancient Greece, Euclid showed that there are infinitely many prime numbers, so it was not discarded the twin prime conjecture was also true. In April 2013, the Chinese-American Yitang Zhang announced that there are at least infinitely many primes separated by a gap of 70 million. This shocked everyone, since Yitang used one of the most difficult methods to achieve his result (he made an improvement to the Goldston–Graham–Pintz–Yıldırım result) and also he was considered an “unknown” number theorist in the international community of mathematicians at the time. Months later, a young man named James Maynard achieve to bound the gap to 600: this mathematician received the Fields medal in 2022 for this achievement and other contributions he made after it. Immediately, the best mathematicians in the world got together under the Polymath Project led by Terence (Terry) Tao who is one of the best current active mathematicians. In a joint effort over months they brought the gap down to 246 and since then, no significant progress has been made beyond. The author using a site (Wolfram Alpha) that links artificial intelligence and mathematics, achieved a calculation that concludes after certain arithmetic steps that the twin prime conjecture is actually true (i.e. he reduced the current gap from 246 to the minimum, which is 2, ending the quest to improve the result).
https://www.linkedin.com/pulse/p-versus-np-frank-vega/
In 1955, the well-known mathematician John Nash wrote to the United States National Security Agency about a problem that had major implications for security and scientific development. A short time later Gödel, one of the most important mathematical logicians, came to the same conclusion and wrote a letter to John von Neumann explaining about the same problem and its relation to computational and mathematical topics. John von Neumann had a successful career in this field at that time: unfortunately he promptly died of cancer and Gödel’s letter was never answered. It took decades later for the American mathematicians Stephen Cook and Russian Leonid Levin could be able to independently introduce and formulate this problem during the “scientific race” of the Cold War. The problem was called P versus NP and it consisted of knowing whether computers were capable or not of solving problems that seemed unfeasible with the computers of that time. The wheel of time passed and these problems are still not feasible to be solved by current computers despite being more powerful. The problem has been extensively studied and is now known to potentially cure cancer if a positive solution is found. Not only this, the disasters caused by the earthquakes in Syria and Turkey could have been predicted and avoided, artificial intelligence tools would achieve their full potential within the recent advances and would also have important industrial and social value since many current flow processes depend on computers. The author found a non-constructive solution (that is, focused on a theoretical answer rather than a practical one) that seems to be feasible not only in speed but also in memory efficiency.
https://www.linkedin.com/pulse/riemann-hypothesis-frank-vega/
The Riemann hypothesis is considered the holy grail of mathematics. The eminent mathematician David Hilbert once said: “If I were to awaken after having slept a thousand years, my first question would be: has the Riemann Hypothesis been proven?” In 1913, Grönwall found what is known today as the Grönwall’s function. Years later, the great Ramanujan found that this function had a certain relationship with the Riemann hypothesis. Since then, Ramanujan began to study certain numbers of which his own tutor Hardy commented to a colleague, confessing: “Even Ramanujan could not make highly composite numbers interesting.” Ramanujan had a very long manuscript on highly composite numbers but some of it was not published until they were found stored in a Cambridge library at the end of the 20th century. During all those years, the prolific mathematician Erdős rediscovered the properties of these numbers and they began to be called colossally abundant numbers. The French mathematicians Robin and Nicolas developed during their research a closer relationship between colossally abundant numbers and the Riemann hypothesis. At the beginning of this century, Nicolas, who was also a close collaborator with Erdős, revealed the importance of an extraordinary number that he called hyper abundant number which belongs to the colossally abundant numbers. The author found another close relationship between the Riemman hypothesis and the colossally abundant numbers with hyper abundant numbers using the Grönwall’s function which announces that the Riemann hypothesis is indeed true.
We prove that the Riemann hypothesis is true when there exist infinitely many hyper abundant numbers n with any parameter u ⪆ 1. We claim that there could be infinitely many hyper abundant numbers with any parameter u ⪆ 1 and thus, the Riemann hypothesis would be true.
https://www.qeios.com/read/ZJNVF8.2
All Magic of Math:
Three possible groundbreaking proofs about two breakthrough problems:
The Riemann Hypothesis and Twin Prime Conjecture
All in once for only those humble enough to read and enjoy them:
https://allmagicofmath.blogspot.com/search/label/All