Contraction and Explosion
Different ways of recursing on graphs

|
| Bletchley Park 2017 source |
William Tutte was a British combinatorialist and codebreaker. He worked in a different group at Bletchley Park from that of Alan Turing. He supplied several key insights and algorithms for breaking the Lorenz cipher machine. His algorithms were implemented alongside Turing’s on Colossus code-breaking computers.
Today we discuss graph recursions discovered by Tutte and Hassler Whitney.
Tutte wrote a doctoral thesis after the war on graph theory and its generalization into matroid theory. We will follow the same arc in this and a followup post. He joined the faculty of the universities of Toronto and then Waterloo, where he was active long beyond his retirement.
For more on Tutte and his work, see this article and lecture by Graham Farr, who is a professor at Monash University and a longtime friend of Ken’s from their Oxford days. We covered some of Tutte’s other work here.
Deletion and Contraction
The two most basic recursion operations are deleting and contracting a chosen edge in a given graph
:

These operations produce graphs denoted by and
, respectively. A motive for them harks back to Gustav Kirchhoff’s counting of spanning trees:
-
A spanning tree of
avoids using edge
if and only if it is a spanning tree of the graph
with
deleted.
-
A spanning tree of
uses edge
if and only if the rest of it is a spanning tree of the graph
after contracting
.
Well, this is not how Kirchhoff counted trees. Counting via the recursion would take exponential time. Our whole object will be telling which cases of the recursions can be computed more directly.
Note that contracting one edge of the triangle graph produces a multi-graph
with one double-edge. Then contracting one edge of
yields the loop graph
.

Thus contraction yields non-simple undirected graphs, but the logic of counting their spanning trees remains valid.
The order of edges does not matter as long as one avoids disconnecting the graph, and the base case is a tree (ignoring any loops) which contributes .
Tutte’s Polynomial
A similar recursion counts colorings that are proper, meaning that for each edge
,
.
-
A proper coloring
of
makes
iff it is a proper coloring of
.
-
A proper coloring
of
makes
iff it induces a proper coloring of
.
This leads to the recursive definition of the chromatic polynomial:
The base cases are that an isolated vertex contributes , whereas an isolated loop contributes
since its single edge is never properly colored. The final rule is that
is always the product of
over all connected components
of
. Then
counts the number of proper
-colorings.
This is like the recursion for coutning spanning terees except for the minus sign. Tutte’s brilliant insight, which was anticipated by Whitney in less symbolic form, was that the features can be combined by using two variables and
. Call an edge a bridge if it is not part of any cycle. If
is not a bridge, the recursion is
The base case is now a graph with some number
of bridges and some number
of loops, which gives
. An important feature is that all
-vertex trees have the same Tutte polynomial
, since there are
edges and they are all bridges. The following are just some of the beautiful rules that
follows. Let
stand for the number of connected components of
.
-
counts the number of spanning trees forests. This counts the number of spanning trees if
is connected.
-
, when multiplied by
, yields the chromatic polynomial.
-
counts the number of spanning subgraphs.
-
is just
.
-
gives the Jones polynomial of a knot related to
.
There are many further relations. The Jones polynomial has many applications including in quantum physics.
Contraction With a Twist
Recall our definition of the “amplitude” of an undirected
-vertex graph
from the “Net-Zero Graphs” post:
where is the number of black-and-white 2-colorings that make an even number of edges have both nodes colored black, and
for an odd number.
There does not seem to be a simple recursion for from
and
. We can, however, obtain one by using another kind of contraction that adds a loop at the combined vertex:

We denote this by . We have not found a simple reference for this. We obtain the following recursive formula:
This recursion allows to be a bridge, so the base cases are
for an isolated vertex and
for a loop. More generally, the basis is
for a node with an even number of loops,
for odd. Here is an example for the ‘star graph’
on 4 vertices:

The diagram would need another layer to get down to (products of) base cases, which we have shortcut by putting values of for each graph
at a leaf. Adding the products over all branches gives
. For the star graph,
Clearly this brute-force recursion grows as . This is slower than the order-
time of using the coloring definition directly, but what all this underscores is how singular it is to be able to compute
in polynomial time, indeed
time. The search for a more-efficient recursion, one that might apply to
-hard quantities, leads us to consider a more-drastic operation on edges.
Exploding Edges
The new recursion operation is well illustrated by this figure:

Two vertices disappear, not just one. Not only does the edge disappear, but any other edge incident to
or
from a vertex
gets “recoiled” into a loop at
. We denote this operation by
to connote that
is not just deleted but “exploded.”
Properly speaking, we need to specify what happens if there are other edges between and
or loops at
or
. In an upcoming post we will see that those become circles in a graphical polymatroid which generalizes the notion of a graph. For now, however, it suffices to let
be the total number of vaporized edges, including
. Then we obtain a two-term recursive formula:
The base cases for isolated vertices are the same as before, but explosion also needs a base case for pure emptiness. This contributes . In the following example diagram, for the path graph
on four nodes, we denote such base cases by `w’ for “wisp”:

Note again the rule that when the recursion disconnects the graph, the component values multiply together. Thus the value is
This is different from the amplitude of the star graph. What this means is that
does not obey the rules of the Tutte polynomial, which is the same for both of these 4-vertex trees.
To prove the recursion equation (1), for , note that every coloring has the same odd/even parity of black-black edges for
as for
except those that color both
and
black. Let
denote the colorings among the latter that make an even number of black-black edges (including
) overall,
for an odd number. Then
Now if there are no other edges between or loops at and
, then
is the same as the number of colorings of
that make an even number of black-black edges, and
becomes the odd case in
again because we subtracted
. Considering the sign change from other
edges or loops and
yields equation (1). It is also possible to “explode” a loop, and our readers may enjoy figuring out how to define it.
The Amplitude Polynomial
We can expand on this by defining a polynomial such that
. The base cases are
for an isolated vertex but still
for a “wisp” and
for a loop. The basis extends to give
for an isolated node with an even number of loops and
for odd. Another way to put it is that two edges with the same endpoints, or two loops at the same node, can be removed. The above diagram shows that for the path graph
,
Whereas, the recursion for the star graph—noting that the “star” on two nodes is just a single edge—gives:
This is not the same polynomial as , again implying that
is not a specialization of the Tutte polynomial. We will show in the last post in this series that
does specialize the polynomial
introduced in this 1993 paper titled, “A Characterization of Tutte Invariants of 2-Polymatroids” and covered further in this 2006 paper.
Open Problems
What other rules does our “amplitude polynomial” follow? We will explore this in the mentioned upcoming post. What other quantities can it be made to count?
What we called “explosion” is in fact attested as the natural form of contraction for the polymatroids considered in these papers. What further uses might “explosion” have in graph theory apart from polymatroids?


There’s a type of contraction operation that figures prominently in my application of cactus graphs to propositional calculus. It’s a rule of inference I call it the Spike Rule and it has the following shape:
Cactus Graph Spike Rule
I’ll add more links one at a time …
There’s a bit of context here:
☞ Cactus Language for Propositional Logic
The logical operators represented by cactus lobes are called minimal negation operators. There’s more detail about them here:
☞ Minimal Negation Operator
Surely, the photograph of Tutle should be tagged with the 1940’s rather than the date of his posthumous centenary celebration in 2017!
The source page dates to 2017 and was the 2017 celebration. We try to make the caption text line up with the desired photo size if possible…
Why does the brute-force recursion give ? It seems to me that you allow multiple loops on the same vertex, but this is unnecessary, it’s enough to count the parity. Wouldn’t this take down the time to
? It seems to me that you allow multiple loops on the same vertex, but this is unnecessary, it’s enough to count the parity. Wouldn’t this take down the time to 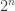 ?
?
The equation has a 3-way branch is all that was meant. Ah, what we wrote is indeed cavalier: on one hand, the first term is recursing on edges not “n” as in vertices; on the other, the recursions might overlap down the road.