Skip to content

Mounting or Solving Open Problems

December 8, 2012
tags: , , , , , , , , , , , , , , ,


Programs not programs

HamiltonClaypic
src

Richard Hamilton is the mathematician who laid out the route that eventually led to the positive solution to the three-dimensional Poincaré Conjecture by Grigori Perelman. He is the Davies Professor of Mathematics at Columbia University. While Perelman famously declined both the Fields Medal in 2006 and the official Clay Millennium Prize recognition in 2010, citing among other factors the lack of concomitant recognition for Hamilton, Hamilton was awarded the Leroy Steele prize in 2009, shared the Shaw Prize in 2011, and had earlier won the 2003 Clay Research Award alongside Terence Tao.

Today Ken and I wish to talk about programs in mathematics, not C++ programs, but programs of attack on a hard open problem. Ken likes the British form “programme” for this.

Hamilton’s brilliant program created a path, a very technical and difficult path, that Perelman was able to ascend. Without this path it is unclear whether the Poincaré Conjecture would have been solved so quickly into the new millennium. The proof of Fermat’s Last Theorem in 1994 also grew out of a far-reaching program named for Robert Langlands’ work and conjectures in the 1960s. The specific program on Fermat via elliptic curves was opened by Gerhard Frey in 1984, and electrified by Ken Ribet’s proof in 1986 of a conjecture that created new connections.

What Is A Program?

A program is not easy to define. I view it a bit like laying out a route for the ascent of a unclimbed mountain. The top of the mountain is the goal, is the solution of the open problem. From the ground the top looks scary, far away, and may seem an impossible climb. Many professional and amateur mathematicians may have tried already to climb to the top, only to fail: some stopped short and returned unhurt, while others fell.

Thus a program in this sense is a potential route to the top of our mountain. From the ground it takes great vision, great insight, and much more, to be able to “see” that a certain route may indeed yield the top of the mountain. Most of us would probably just start climbing and quickly hit a part of the mountain that is an impasse. We get stuck. It looks like this:

04-04Everest_smE918D454_Page
source—“Mount Everest Made Easy”

But Hamilton was an example of those with vision to see a plausible route to the top—-in his case to the solution of the Poincaré Conjecture. Of course, he had partial evidence that his route, his program, made some sense. It was different from previously-tried routes that all had failed. He also could use his route to get at least partial results. Following his route he proved special cases of the Poincaré, which in our metaphor is like reaching a height further up toward the peak of the mountain than anyone else had ever done.

Perhaps the simplest definition of a program is that it is something other than a “program”—at least the type of program we wrote when learning Algol or Pascal or C. Those programs were single procedures to solve an already-determined problem. A program gives a way to “mount” the mountain for analysis, as distinct from the act of solving the problem. We have recently contrasted “object-oriented” programs from procedural ones in this context.

What distinguishes a program is developing a new ingredient and/or approach. This can be a new object, a connection, an expanded battlefield, or a theme developed from more-fundamental scientific principles. A program can have all or some of these—the more, the better.

I hope this helps explain a bit what a program is in this context. let’s turn to look at a few programs. Some have already been successful, others are still pending.

Some Programs

First we look again at the examples introduced above.

{\bullet } Hamilton: Ricci flow—a new object. This idea applies to Riemannian manifolds quite generally, not just the ones used by Perelman.

{\bullet } Langlands: An expanded theatre—as with “programme” Ken likes the British spelling in this context. The first National Academy of Sciences Award in Mathematics recognized his

“extraordinary vision that has brought the theory of group representations into a revolutionary new relationship with the theory of automorphic forms and number theory.”

Of course an expanded theatre brings new connections, but those are often for others to find.

{\bullet } Frey: A new connection via elliptic curves. Sometimes the best way to prove a theorem is to see what you get if it’s false. Consider the elliptic curve

\displaystyle y^2 = x(x + a^n)(x - b^n)

whose right-hand side is a cubic polynomial {p} with distinct roots {0,-a^n,b^n}. The discriminant of a polynomial {p} is the product of the squared pairwise differences of its roots. Here if {a^n + b^n = c^n}, we get for the discriminant:

\displaystyle \Delta(p) = (a^n)^2(b^n)^2(a^n + b^n)^2 = (abc)^{2n}.

Thus an integer solution to Fermat’s equation with {n \geq 3} would create an elliptic curve with the special property that its discriminant is a sixth or higher power of an integer. If {n} is a prime—the only cases needed to prove Fermat—then existing tools in the theory of elliptic curves hinted that the curve would acquire more properties that are “too special”—they self-contradict. For Andrew Wiles to complete the proof, with assistance from Richard Taylor, however required transferring the final problems to another part of Langlands’ theatre, involving Galois representations and class numbers. The curves in this case had actually been found by Yves Hellegouarch, but Frey developed the properties.

{\bullet} Ribet: A new connection, via a new result. When Ribet proved the so-called epsilon conjecture, it completed a path of implication from a conjecture named variously for Goro Shimura, Yutaka Taniyama, and André Weil, clear through to Fermat’s Last Theorem. Wiles did not prove the whole latter conjecture, but enough of it to deduce Fermat. Taylor was part of a team that completed the whole of the work in 2001: the conjecture is now a theorem.

Some Programs in Computational Complexity

In computational complexity we have our own Everest: resolving the {\mathsf{P=NP}} question. But in a sense we haven’t even gotten over the foothills: no one has proved any truly general and meaningful super-linear lower bounds: none on circuit size, nor above the slightest super-linear functions on Turing machine running time. However, it is possible that this landscape is fractal: the whole range may have the same obstacles regardless of height, and scaling one hill may be as hard as opening the path to the top.

There are many programs in our field that we could mention, but we’ll stay with four of the ones that are directed squarely at the peak:

{\bullet } Mike Sipser: Circuit Lower Bounds. I (Ken) like to state the theme as, “Machines have moving parts; circuits don’t.” That is, a circuit is a fixed combinatorial structure, without the dynamic head movements and memory-access patterns of a Turing machine or RAM program. Thus a circuit is a fixed target for lower-bound arguments. One can also easily differentiate the structure of circuits according to depth, fan-in, width, and various connectivity notions.

The “Sipser Program” began auspiciously with strong lower bounds against polynomial-size circuits of constant depth, even allowing unbounded fan-in gates that count modulo some fixed prime number. However, at the level of threshold gates or logarithmic depth it encountered a barrier, one erected almost 20 years ago by Alexander Razborov and Stephen Rudich. The barrier may require cliff-scaling or finding a new base camp, or maybe the premise on which it was erected (the exponential security of pseudorandom generators, including ones based on factoring) isn’t true and we can plow ahead with the program after all.

Despite the stopping of progress, I feel it is wrong to say the program bogged down—rather, it was rocked by several other programs we could equally well highlight: one-way functions (and) pseudorandom generators, hardness versus randomness, even algebraic methods in complexity. This kind of clash is good: programs should impact each other.

{\bullet } Ryan Williams: New ideas for circuit lower bounds: This is a plow-ahead movement, armed with the theme of looking for new upper bounds and expanding the kinds of problems considered—as we tried to style it here. Just this week, he has tackled the relation of his ideas to natural proofs, and has improved his {\mathsf{ACC}} lower bounds.

{\bullet } Ketan Mulmuley: His program of Geometric Complexity Theory expands the theatre in the direction of Langlands, employing group representation theory and deep concepts of algebra. Here is his overview last summer for Communications of the ACM. While the attack is most squarely on Leslie Valiant’s algebraic analogue {\mathsf{VNP \neq VP}} of {\mathsf{NP \neq P}}, which embraces permanent versus determinant, the effects may be tantamount. In his FOCS 2012 paper, he has linked complexity questions to Emmy Noether’s century-old Normalization Lemma.

{\bullet } Michael Freedman: Knot theory and topology. Freedman won a Fields Medal in 1986 for his work on the 4-dimensional case of the Poincaré Conjecture. He has since worked at the juncture of enumerative combinatorics, knot theory, and topology. Problems in these fields are often naturally complete for {\mathsf{PSPACE}} or {\mathsf{PP}}–cum–{\mathsf{\#P}}. This 2008 paper shows a special knot-theoretic consequence of {\mathsf{NP}} being properly contained in {\mathsf{P^{\#P}}}. His program has yielded results on quantum computing, including a proposal for a topological quantum computer, which also relates to {\mathsf{BQP}} versus {\mathsf{PP}}.

Open Problems

While reaching the top of the mountain—solving the open problem—is the most fun, laying out potential programs is of critical importance. I (Dick) think that we need more of the latter in complexity theory. We lack, in my opinion, visionaries who can lay out programs that may succeed. I hope we get more of them in the future.

Atle Selberg once said:

There have probably been very few attempts at proving the Riemann hypothesis, because simply no one has ever had any really good idea for how to go about it!

from → History, Ideas, P=NP
31 Comments leave one →
  1. Jon Awbrey permalink
    December 9, 2012 12:48 am

    Sometimes the program(me) must simply be to keep developing our understanding of the ground on which the mountains rest.

    Reply
  2. mkatkov permalink
    December 9, 2012 8:46 am

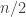    Almost every healthy person can climb Everest today, compared to K2 where not many people were successful. When someone writes a monomial x_1 x_2... x_n someone already lost a lot of information. Even splitting it into exactly n/2 degree components gives (x_1 x_2..x_{n/2})(x_{n/2+1}x_{n/2+2}..x_n)= (x_{n/2+1} x_2..x_{n/2})(x_1 x_{n/2+2}..x_n)= ... or \binom{n}{n/2} \approx exp(n) relationships. Not using it, is the same as trying to go around the mountain on the same altitude.

    Reply
    • KWRegan permalink
      December 9, 2012 2:22 pm

      In poker terms, I’ll call your monomial example and raise you a vector. Call two vectors x,y of length n = 2m “dyadically orthogonal” if [2m] can be partitioned into m-many subsets B of size 2 such that (x_B,y_B) = 0. (If B = {i,j} then y_B = (y_i,y_j); thus the notion is invariant under permutations of the coordinates.) Call a matrix dyadically orthogonal if every pair of distinct columns (equivalently, rows?) are dyadically orthogonal. Has this notion been studied? Do such matrices form a group? Just free-associating in real-time…

      Reply
      • mkatkov permalink
        December 10, 2012 4:09 pm

        One particular example of your matrix is Hadamard matrix http://en.wikipedia.org/wiki/Hadamard_matrix. I guess every Hadamard like matrix with orthogonal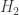 H_2 in Sylvester construction would also satisfy this properties. The last one is only good for 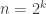n=2^k (and is known as Walsh matrix). I do not know if those are the only examples, since in both Walsh and Hadamard matrices there is an additional requirement that rows are mutually orthogonal.

      • mkatkov permalink
        December 13, 2012 3:34 pm

        associating in real time one can try to construct such matrices. Fix the field, start with a vector of length 2m. Take all 2 covers of vector coordinates, fix their order (it is interesting whether permuting covers order is equivalent to the permutation of coordinates). The second vector in the matrix have to be dyadically orthogonal to the first one. It is easy to obtain. The third vector have to be both dyadically orthogonal to the first vector, and the second vector, etc. e.g. the mutual covers introduce mutual constraints. The contradictory constraints are only possible when the sequence of covers form the closed loop, e.g. when there are 2 different paths (need to be defined here) to the coordinate through the covers. The maximum size of the matrix is defined by the maximum length of not overlapping covers. For these matrices there seems to be no real constraint on the initial vector. If one has overlapping covers there are additional constraint on the initial vector. That may relate to the polynomial Hirsh conjecture discussed by Gil. Through the Hadamard matrices there is possible connection to permanent. Since I do not really understand your free associations, there are many direction this can lead. It is not even clear how many columns can be in the matrix.

      • mkatkov permalink
        January 17, 2013 9:04 am

        Dear Ken, the file below (Mathematica printout) show that you can get Nulstellensatz certificate for factoring ‘0’ into odd factors in 6 variables (3 per factor) of only 8th degree using standard Nullstellensatz proof system, whereas using tautologies one can get certificate of equivalent to 6th degree in the original variables (and it is actually not wider that usual Nullstellensatz certificate). It is still questionable how does this scales with n, but that will be much harder for me to analyse. Someone should take care of it, since I can only grasp elementary math, which will require much longer time to sort out matter.

        http://mkatkov.files.wordpress.com/2013/01/tautologies6vars4thorder1.pdf

        What is interesting here is that with encoding x_k^2=1, the 6th order equations in tautologies are providing nullspace corresponding to all 64 possible values for the variable, which is not the case for Nullstellensatz proof system. So, any six-covering of the variables provide corresponding null space, and you do not need to increase certificate degree above six. The problem is to encode the problem that is also cover this null space without singularly (e.g. encoding kernel is not in the nullspace of solutions), and still have polynomialy wide sixth degree encoding.

        I apologize, that I cannot formalize all the above, and that sounds as a bullshit. I would appreciate any references, dealing with similar stuff.

    • mkatkov permalink
      February 19, 2013 6:55 am

      I still do not understand, is it very hard to provide keywords, if not references. The monomials example seems to fall into “Determinantal rings” and
      “Determinantal rings and varieties have been a central topic of commutative algebra
      and algebraic geometry.” is the first sentence from http://www.home.uni-osnabrueck.de/wbruns/brunsw/detrings.pdf

      Reply
  3. André Luiz Barbosa permalink
    December 9, 2012 4:36 pm

    About this theme, see the visionary visions at http://arxiv.org/ftp/arxiv/papers/0907/0907.3965.pdf, like the new NP genealogy.

    Reply
  4. John permalink
    December 10, 2012 3:15 am

    when a lie is being repeated 1000 times it eventually becomes truth.. or at least this is what the author of this blog post seems to think

    Reply
    • Wim van Dam permalink
      December 10, 2012 3:58 pm

      Care to explain why you wrote this?

      Reply
      • john permalink
        December 20, 2012 8:53 am

        For what it’s worth, I take this back.

    • André Luiz Barbosa permalink
      December 12, 2012 1:24 pm

      “How many roads must a man walk down before you call him a man?” (Bob Dylan)

      Reply
  5. Arnab permalink
    December 11, 2012 8:51 am

    What about the combined area of probabilistic proof systems, and theories on bounds on approximation? Can that be considered something like a “programme” ? Possibly with no single creator’s name, such as Langland or Connes. Or perhaps – it can be traced back to your work on program checking? Like in physics, Leonard Susskind is known as the father of string theory for many initial ideas.

    Reply
  6. varasdemate permalink
    December 11, 2012 9:30 am

    Reblogged this on varasdemate and commented:
    Very interesting article on recent developments concerning solving open problems.

    Reply
  7. Bill Gasarch permalink
    December 12, 2012 8:37 pm

    One result is a paper
    Two results is a sequence of papers
    Three results is a PhD thesis or book
    Four results is a program

    When you start a program its hard to know where on this list
    it will end.

    Reply
  8. Anonymous permalink
    December 13, 2012 1:44 am

    There is also Cook’s program in proof complexity for showing NP is not equal to coNP.

    http://www.math.ucsd.edu/~sbuss/ResearchWeb/lfcsSurvey/

    Reply
    • Serge permalink
      December 13, 2012 9:26 am

      There seems to be a general principle related to computer languages. The low-level ones – being “close to the machine” – yield programs whose efficiency’s easy to assess but whose correctness is more difficult to prove. In this category are e.g. assembly language and a system language such as C. By contrast the more high-level languages – being “far from the machine” – yield programs with the opposite properties. Their complexity’s harder to assess but their correctness can be proved more readily. In this category are the functional languages such as Haskell, Ocaml, Clojure and so on.

      I think mathematicians who try to separate some complexity classes by means of an algorithm are confronted with a similar phenomenon. Sometimes they have a fast algorithm that they can’t prove correct… and some other times their algorithm is known to be correct but is probably not the fastest one. This is how I understand Kreisel’s opinion – quoted in Samuel Buss’s above-mentioned paper – that “under reasonable conditions on feasibility, there’s an analogue to Gödel’s second incompleteness theorem”.

      Reply
  9. Jon Awbrey permalink
    December 13, 2012 9:22 am

    As long as we’re brainstorming in a laid back sort of way …

    Folks who find propositional logic — and the whole space between zeroth order logic and first order logic — more of a fascinating playground for exploration than a dog walk for the questying beast might find it fun to look at the graph-theoretic calculi for propositions and boolean functions that derive from C.S. Peirce’s logical graphs, There is an extension of Peirce’s tree-form graphs to cactus graphs that presents many interesting possibilities for efficient expression and inference. And the resulting cactus calculus facilitates the development of differential logic, extending propositional calculus analogous to the way that differential calculus extends analytic geometry.

    Links to follow in the next post …

    Reply
  10. Jon Awbrey permalink
    December 14, 2012 1:06 pm

    It might be observed that the concept of a research programme is closely related to the concept of a research paradigm. About which much has been written.

    Reply
  11. Gil Kalai permalink
    December 25, 2012 4:23 pm

    Another program in mathematics is the Zimmer programm: http://chicagomaroon.com/2010/03/05/the-zimmer-program/.

    Reply
  12. Jon Awbrey permalink
    January 4, 2013 11:46 am

    (Note. I’m having trouble posting links that go outside the WordPress system, so I’ll redo the intended link as an indirect link below.)

    Re: “Working on his Ph.D. at Harvard in the early ‘70s, Zimmer was interested in the relationship between dynamics, the study of repeated transformations, and Lie theory, an area of algebra that studies symmetries.”

    When it comes to programs for “developing our understanding of the ground on which the mountains rest”, there is every reason to believe that the differential extension of propositional calculus would open up new prospects. I’ve recorded a sample of my own excavations in the following paper.

    See the paper titled “Differential Logic and Dynamic Systems” on this page.

    Reply
  13. vznvzn permalink
    February 18, 2014 11:52 am

    hi RJL this is one of my fave blogs of yours & really like the visionary aspects of theory partly encompassed by the informal yet critical idea of “Research Programs” which are somewhat rarely directly referenced or appreciated in all their wide vistas by the more common/standard micro/incremental specialists working in many branches of science (but are perhaps often assumed)… it addresses the critical issue of motivation/background in research….

    its also interesting to contrast how Polymath has some interplay with research programs.

    would like to announce two new Research Programs here!

    SAT induction is based on reducing computational or mathematical questions to a (infinite) series of SAT formulas, looking for a common pattern in those formulas truth/falsity, and using it to create inductive proofs. its a variant of automated theorem proving. think it is quite promising. formulated the idea many yrs ago but have a somewhat clearer picture now & there are some related results in the literature to cite now.

    outline for P vs P/Poly proof based on monotone circuits, hypergraphs, and factoring … have mentioned this one before however have some new ideas/refs based on hypergraph decompositions, have to write that blog up sooner or later…

    hope to hear from anyone esp sr researchers! 😀

    Reply

Trackbacks

  1. Paradigms, Playgrounds, Programmes, Programs | Inquiry Into Inquiry
  2. Demonstrative And Otherwise | Inquiry Into Inquiry
  3. How to Prove Fermat’s Little Theorem | Eventually Almost Everywhere
  4. solitons, cellular automata, quantum mechanics, and disagreeing with scott aaronson | Turing Machine
  5. P vs NP Proof Claims | Gödel's Lost Letter and P=NP

Leave a Reply

Discover more from Gödel's Lost Letter and P=NP

Subscribe now to keep reading and get access to the full archive.

Continue reading